Cap. 7 Test de Hipotesis y Pruebas No paramétricas
En estadística se plantean siempre dos tipos de hipótesis
Una hipótesis nula: H0 (de no efecto)
Una hipótesis alternativa: H1 (de diferencia o efecto)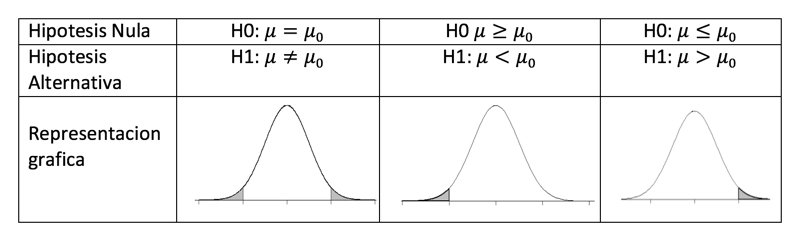
Figura 7.1: Planteamiento de Hipótesis
7.1 Test de Hipótesis de Una Variable e Intervalos de Confianza
Distribución z (Cuando la varianza es conocida)
R no posee los comandos para desarrollar esta prueba de manera directa.
La forma estadística para probar una media de datos con varianza conocida es:
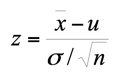
La mejor forma de obtener el estadístico es desarrollarla de forma simple.
7.1.1 Ejemplo 7.1.
Se esta interesado en obtener una estimacion del peso, de una especie de ave en una cierta poblacion que se ubica en una zona seca. Se toman 27 muestras de forma aleatoria de la misma especie y se determina el peso para cada una de ellas. El peso medio reportado fue de 37.4 gramos con una varianza de 25. Supongase que los datos asumen una distribucion aproximadamente normal.
- Es posible concluir que el peso medio de las aves de esa población sea igual a 40 gramos.
xbar=37.4
n = 27
mu = 40
var = 25
z<-(xbar-mu)/(var/sqrt(n))
z## [1] -0.54Dado que el valor z al 95% de confianza, no cae fuera del área de aceptación (mas menos 1.96), se acepta el H0.
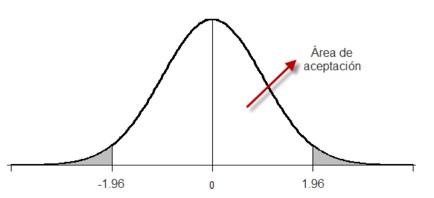
Figura 7.2: Planteamiento de Hipótesis
R/ podemos concluir que el peso medio de las aves es igual a 40 gramos. (z=-0.54; gl=26; P>0.05) al 95% de confianza.
Para calcular el valor de p.
dnorm(-0.5403999)## [1] 0.345El valor de la p es de 34,47%, que es la probabilidad de que ocurra el evento.
Si se nos hubiera planteado lo siguiente.
- Es posible que el peso medio de las aves sea menor de 39?:
xbar=37.4
n<-27
mu<-39
var<-25
z<-(xbar-mu)/(var/sqrt(n))
z## [1] -0.333pnorm(-.3325538) #se obtiene el valor de la probabilidad.## [1] 0.37R/ podemos concluir que el peso medio de las aves no es menor a 39 (z=-0.33;gl=26; P>0.05) al 95 % de confianza.
El valor de la p es de 36.97%, corresponde a la probabilidad de que ocurra el evento.
7.2 Distribucion t- student (Cuando la varianza es desconocida)
El t-test es basado en el supuesto de que sus datos provienen de una distribución normal, los datos son continuos, y la muestra es tomada en forma aleatoria de la población.
La función matemática que describe la distribución t-student esta dada por:

revisamos los parámetros de t.test
?t.testRecuerde que cuando se conoce el sigma de la población el estadístico a aplicar es z.
El t-student permite ademas, calcular los intervalos de confianza de la población. Normalmente se trabajan al 95% y 99%. En otras áreas puede trabajar en otros tipos de intervalo (96%, 97%, etc).
Los intervalos de confianza contienen información del posible error en la estimación a través de la dispersión y de la distribución muestral del estimador. El error en la estimación esta directamente relacionado con la distribución muestral del estimador y con la varianza poblacional, e inversamente relacionado con el tamaño muestral.
Los intervalos de confianza de un parámetro poblacional desconocido nos brindan una idea de la precisión y exactitud de la inferencia obtenida. Es decir, es mas valido en Biostadística decir, que tenemos una población x en vida silvestre cuyo tamaño es de 100 mas menos 13 individuos a decir que, hay exactamente 100 individuos, cuando en la realidad lo que estamos brindando en una aproximación de la estimación. El intervalo de confianza nos permite, estar entre el error posible del parámetro estimado, en nuestro caso esperaríamos entre 87 a 113 animales y no 100 exactamente.
Para proceder con el uso de t-student es necesario previo al análisis aplicar la prueba de normalidad.
7.3 Test de la Distribución Normal
Uno de los supuestos que debemos de tratar en este tipo de prueba es el de distribución normal. Utilizaremos para ello el estadístico de Shapiro-Wilk, existen otros estadísticos que pueden también utilizarse para probar la distribución normal.
shapiro.test(x) # donde x son los valores de un vector de datos numéricos
7.4 t.test para una muestra
El estadístico aplicado es el t-student. Recomendado para trabajar con muestras pequeñas. Sin embargo, cuando se trabaja con muestras grandes los datos son próximos a una distribución aproximadamente normal.
7.4.1 Ejemplo 7.2.
Se realiza un experimento donde se midio la produccion de vainas de frijol por cada mata producida, en 12 unidades experimentales sometidas bajo las mismas condiciones.
mf<- c(18,11,17,10,20,25,13,16,25,20,19,20)Probamos el supuesto de normalidad de nuestros datos
shapiro.test(mf)##
## Shapiro-Wilk normality test
##
## data: mf
## W = 0.9, p-value = 0.5Hipótesis
H0= Los datos provienen de una distribución normal H1: Los datos presentan una distribución asimétrica.
Aceptamos H0: Nuestros datos cumplen con el supuesto de normalidad.
7.4.2 Estime el intervalo de confianza al 95% para el rendimiento promedio del numero de vainas producidas por cada mata de frijol. Los datos presentan una distribucion normal.
Solución:
El intervalo de confianza es construido a través de la prueba t.test (x)
t.test(mf)##
## One Sample t-test
##
## data: mf
## t = 10, df = 10, p-value = 6e-08
## alternative hypothesis: true mean is not equal to 0
## 95 percent confidence interval:
## 14.8 20.9
## sample estimates:
## mean of x
## 17.8El intervalo de confianza al 95% obtenido es: [14.78 a 20.88], lo que representa es el intervalo de la media de la población de las vainas de frijol. Así mismo se obtienen otros resultados como la media de la muestra de: 17.83.
Se nos brinda información adicional del valor calculado de t=12.86, los grados de libertad (df=11), obtenidos de la formula gl=n-1 (numero de observaciones menos uno), y la probabilidad resultante (p-value = 5.673e-08), en nuestro caso es menor a 0.05, por lo que nuestro resultado es significativo dado la hipótesis por defecto.
H0: media igual a 0
H1: media es diferente de 0
alternative hypothesis: true mean is not equalto 0: significa solo el planteaiento de nuestra hipótesis alternativa (la media es diferente de cero), y no se refiere a una conclusión de nuestros resultados.
7.4.3 Construya un intervalo de confianza al 99% de confianza para el rendimiento promedio de la de vainas producidas por cada mata de frijol.
t.test(mf, conf.level=0.99)##
## One Sample t-test
##
## data: mf
## t = 10, df = 10, p-value = 6e-08
## alternative hypothesis: true mean is not equal to 0
## 99 percent confidence interval:
## 13.5 22.1
## sample estimates:
## mean of x
## 17.8Respuesta: Tengo una confianza al 99% que la media de la población se encuentra entre [13.52 a 22.13] vainas de frijol por cada mata.
7.4.4 Supongamos que deseamos verificar la siguiente hipotesis estadistica: el numero de vainas producidas por mata de frijol, es diferente de 23, al 99% de confianza.**
- Como plantearía su hipótesis?
t.test(mf,mu=23, alternative="two.sided", conf.level = 0.99)##
## One Sample t-test
##
## data: mf
## t = -4, df = 10, p-value = 0.003
## alternative hypothesis: true mean is not equal to 23
## 99 percent confidence interval:
## 13.5 22.1
## sample estimates:
## mean of x
## 17.8Respuesta: el numero de vainas producidas por mata es diferente de 23, de manera significativa (t = -3.72; gl = 11; p-value = 0.003 o P<0.01).
7.4.5 Supongamos que deseamos verificar la siguiente hipotesis: el numero de vainas producidas por mata es mayor que 23, al 99% de confianza.**
- Como plantearía su hipótesis?
t.test(mf, mu=23, alternative="greater", conf.level = 0.99)##
## One Sample t-test
##
## data: mf
## t = -4, df = 10, p-value = 1
## alternative hypothesis: true mean is greater than 23
## 99 percent confidence interval:
## 14.1 Inf
## sample estimates:
## mean of x
## 17.8Respuesta: el numero de vainas producidas por mata es menor o igual a 23 a un 99% de confianza, de manera no significativa (t = -3.72; gl = 11; p-value = 0.99).
7.4.6 Suponga que se desea conocer que: si, el numero de vainas producidas por mata es menor de 6, al 95% de confianza.**
- Como plantearía su hipótesis?
t.test(mf,mu=6, alternative="less", conf.level = 0.95)##
## One Sample t-test
##
## data: mf
## t = 9, df = 10, p-value = 1
## alternative hypothesis: true mean is less than 6
## 95 percent confidence interval:
## -Inf 20.3
## sample estimates:
## mean of x
## 17.8Respuesta: el numero de vainas producidas por mata de frijol no es menor que 6, de manera no significativa (t = 8.53; gl = 11; p-value = 1), al 95% de confianza.
Nota: Revise siempre sus datos que sean simétricos (para ello puede generar un histograma) y que ademas, no presenten datos extremos (en el mayor de los casos, aunque esto no es un problema, mas que el tipo de distribución que se ajusta), esto resulta fácil de observar a través de un boxplot.
En nuestro caso los datos parecen ser simétricos y no presentar datos extremos (outlier), (Figura )
par(mfrow=c(1,2))
mf<- c(18,11,17,10,20,25,13,16,25,20,19,20)
mean(mf)## [1] 17.8boxplot(mf,col="gray85", main="Standard\nBoxplot")
points(mean(mf), pch=20, cex = 1.5)
text(17.5, "Promedio", col="red", font=8 )
median(mf)## [1] 18.5text(19, "Mediana", font=8)
quantile(mf)## 0% 25% 50% 75% 100%
## 10.0 15.2 18.5 20.0 25.0text(14, "Cuantil 1", font=8)
text(20.4, "Cuantil 3", font=8)
hist(mf)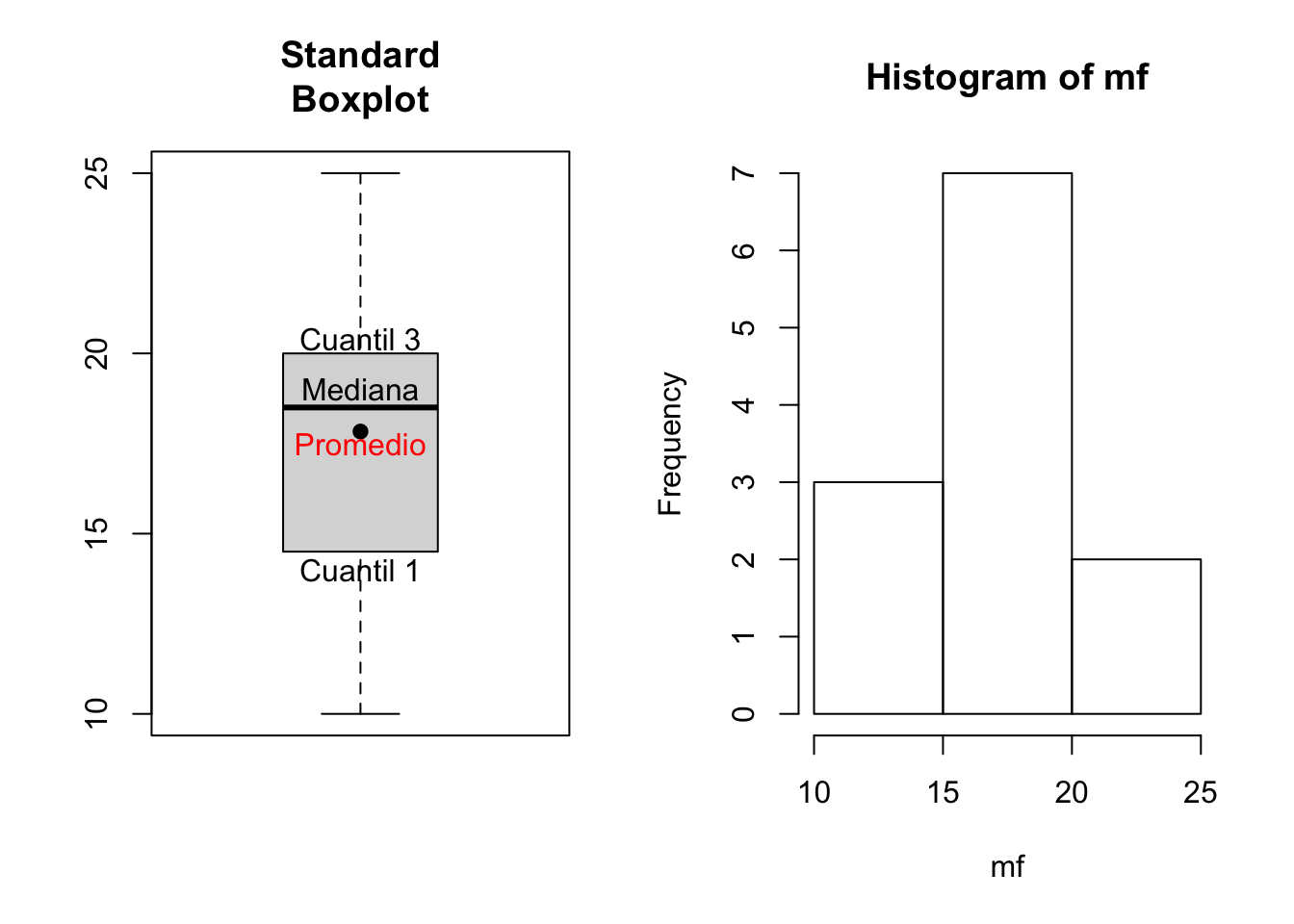
Figura 7.3: Boxplot e histograma de frecuencia para ver la simetría (hist) y existencia de datos extremos (boxplot).
Recuerde siempre visualizar los valores en cuanto a estadísticas descriptivas para dar un reconocimiento previo de sus datos. Recomendamos para esta ocasión instalar el paquete resumeRdesc: https://github.com/osoramirez/resumeRdesc. La ventaja de este paquete es que arroja una serie de estadística de forma automática, ademas de una sección gráfica.
library(resumeRdesc)resume(mf)## [1] "You got Normal distribution."
## [1] "Warning: You have a low sample size (n<30)"
## [1] "You do not have outlier"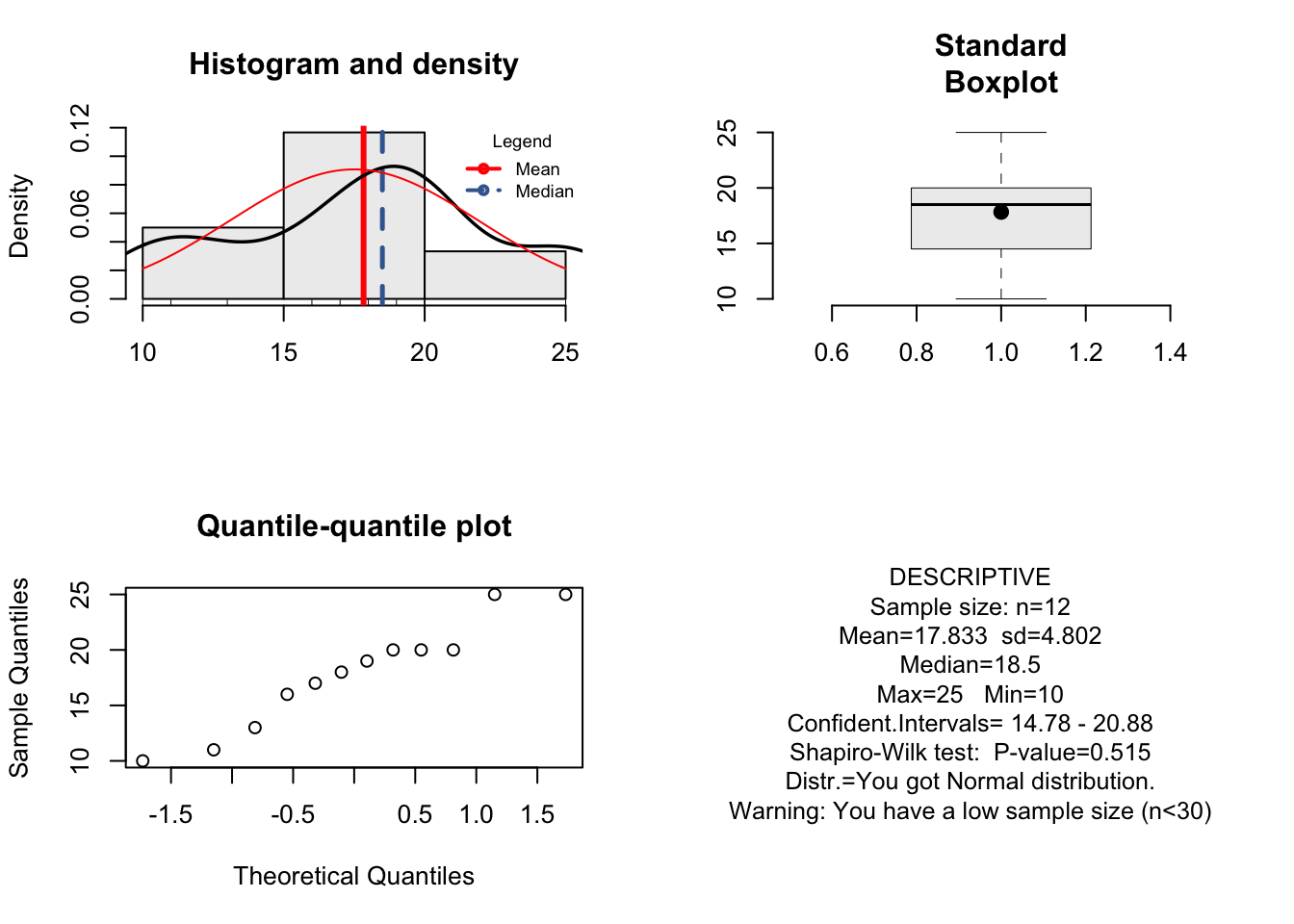
Análisis gráfico exploratorio de resume2data (resumeRdesc)
7.4.7 Genere 100 numeros aleatorios con distribucion normal, con una media de 15, cuya desviacion estandar sea de 4.65.
7.4.8 Calcule el intervalo al 95% de confianza de los 100 datos aleatorios con distribucion normal.
set.seed(12345)
rnorm(100,mean=15, sd=4.65)->x
t.test(x)##
## One Sample t-test
##
## data: x
## t = 30, df = 100, p-value <2e-16
## alternative hypothesis: true mean is not equal to 0
## 95 percent confidence interval:
## 15.1 17.2
## sample estimates:
## mean of x
## 16.1par(mfrow=c(1,2))
boxplot(x,col="gray85", main="Standard\nBoxplot")
hist(x, main="Histrograma\nDatos", col="gray85")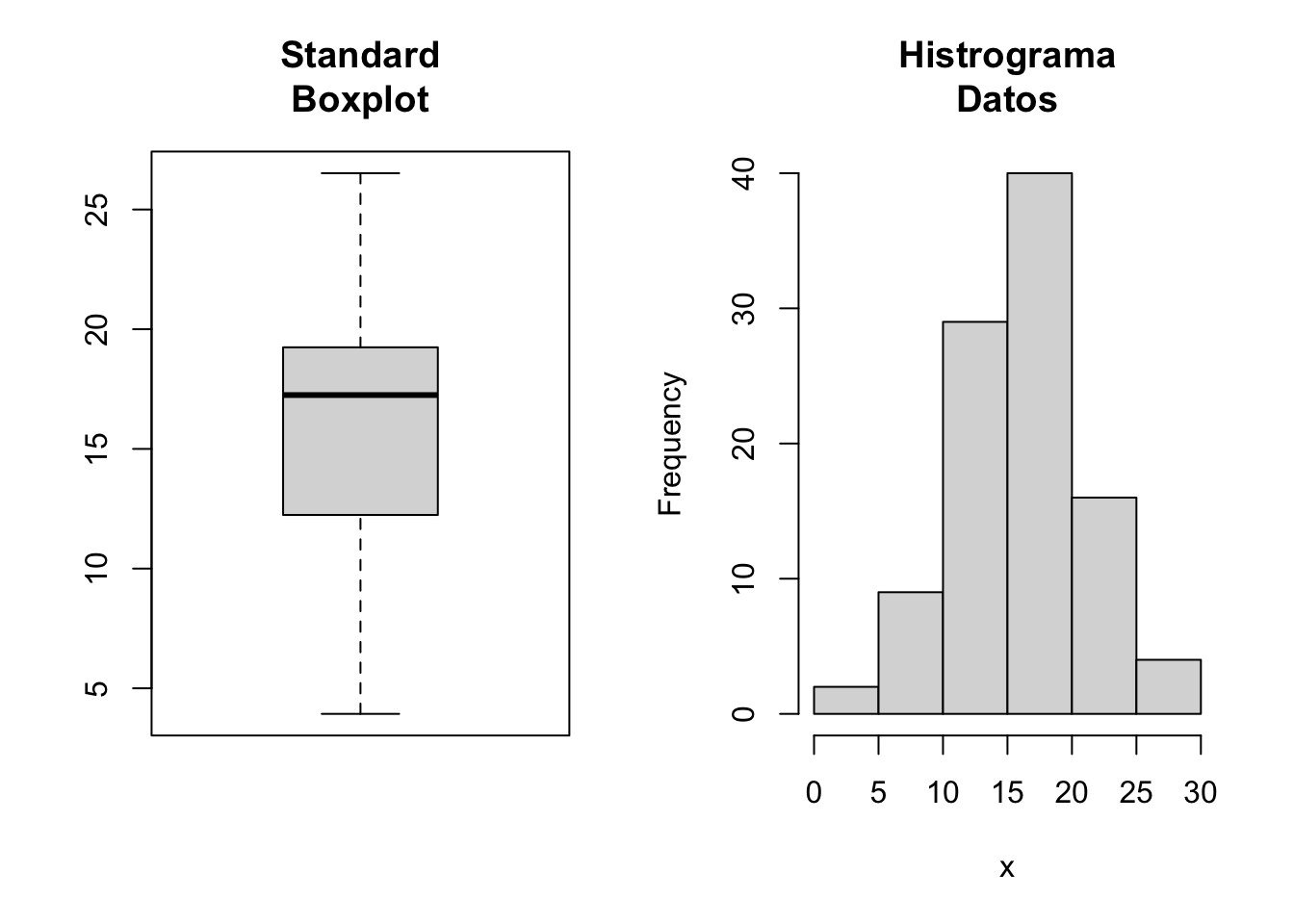
Figura 7.4: Boxplot e histograma de frecuencia para ver la simetría (hist) y existencia de datos extremos (boxplot)
R/ el intervalo de confianza al 95% de la variable aleatoria de x es de [15.11 a 17.16].
7.5 Test de Wilcoxon
Se utiliza como alternativa a la prueba de t-student, cuando no se cumple con el supuesto de la distribución normal de los datos. Al no cumplir con este supuesto se vuelve una prueba no paramétrica. Las estadísticas no paramétrica prueban hipótesis respecto a la mediana y no a la media.
El test de Wilcoxon, se aplica en mediciones en escala ordinal para muestras dependientes.
El test de Wilcoxon, compara la mediana de una o dos poblaciones de muestras relacionadas y determina si existen diferencias entre ellas.
?wilcox.test7.6 Test de Wilcoxon para una muestra
Nota: utilice exact = FALSE, cuando se trata de muestras menores a 50.
7.6.1 Se cuentan en una parcela experimental, la cantidad de maleza producida por metro cuadrado en una plantacion de maiz. Los datos son los siguientes.**
7.6.2 Se quiere saber si la cantidad de maleza por metro cuadrado es mayor a 10.
library(resumeRdesc)
ma<-c(1,3,6,4,18,11,6,6,3,4,2,5,5,4)
resume(ma)## [1] "You got Asymmetrical Distribution"
## [1] "Warning: You have a low sample size (n<30)"
## [1] "Warning: You have outlier"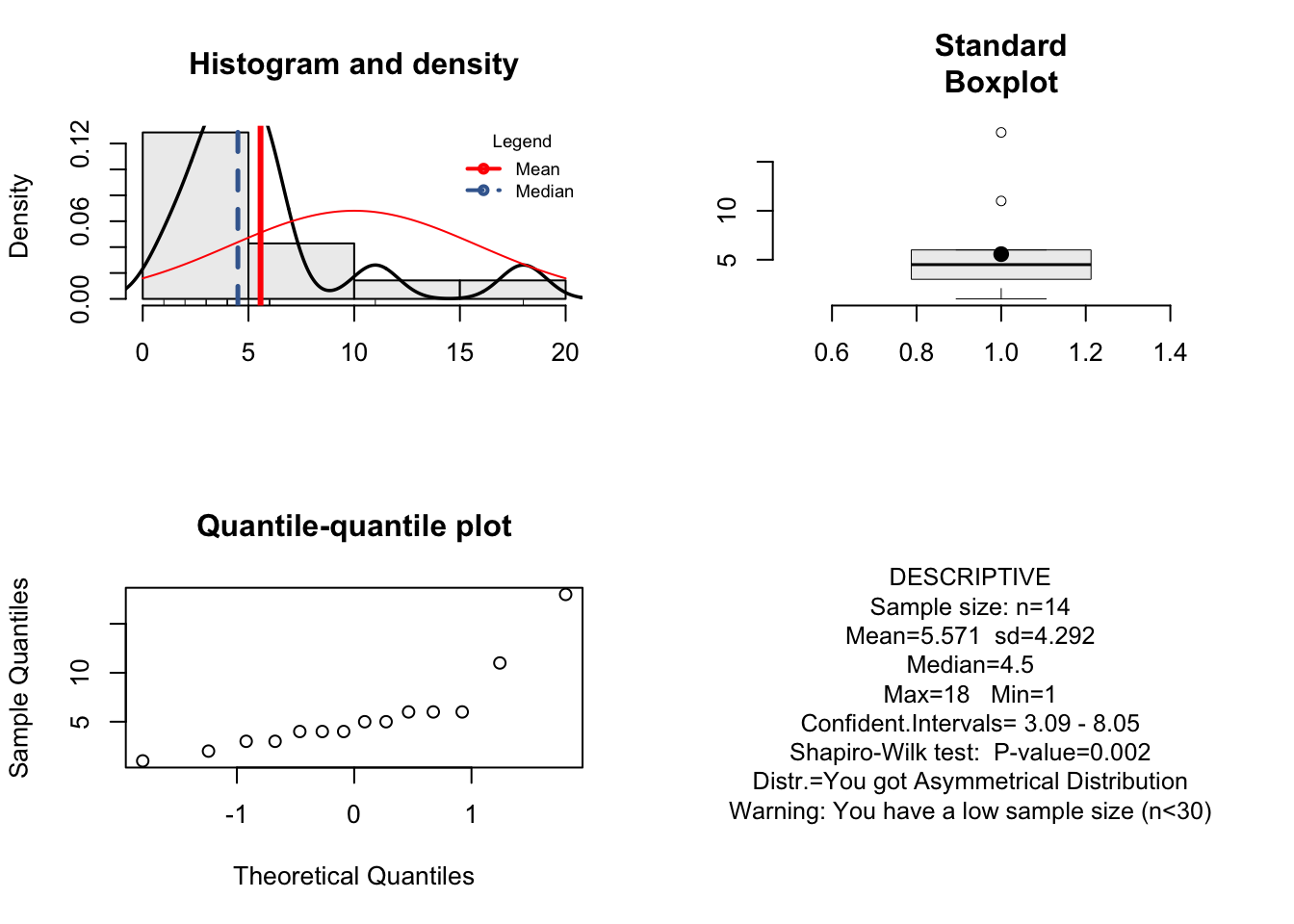
shapiro.test(ma)##
## Shapiro-Wilk normality test
##
## data: ma
## W = 0.8, p-value = 0.002Como se observa podemos utilizar el test de Wilcoxon, debido a que los datos no presentan normalidad. Así mismo los datos presentan outlier y no son simétricos.
wilcox.test(ma, mu=10, alternative = "g", exact = FALSE)##
## Wilcoxon signed rank test with continuity
## correction
##
## data: ma
## V = 10, p-value = 1
## alternative hypothesis: true location is greater than 10R/. La cantidad de malezas producida por metro cuadro no es mayor a 10 (Wilcoxon=13.5; gl=13;p-value=0.99).
7.6.3 Se lleva a cabo una encuesta, donde se les solicita a pacientes de un hospital, que califiquen la atencion que se les ha brindado en dicha institucion. Se clasifican las respuestas utilizando una escala de 1 a 10, donde 10 denota la mejor calificacion. Los datos son los siguientes.
7.6.4 El administrador desea sabe si la respuesta de calificación media obtenida es mayor a 7.
x<-c(3,6,2,8,8,6,5,8,4,8,3,4,2,6,4,8,4,7,4,5,9,2,3,2,4,2,7,6)resume(x)## [1] "You got Asymmetrical Distribution"
## [1] "Warning: You have a low sample size (n<30)"
## [1] "You do not have outlier"
shapiro.test(x)##
## Shapiro-Wilk normality test
##
## data: x
## W = 0.9, p-value = 0.03wilcox.test(x, alternative="greater", mu=7, conf.level = 0.95,exact = FALSE )##
## Wilcoxon signed rank test with continuity
## correction
##
## data: x
## V = 40, p-value = 1
## alternative hypothesis: true location is greater than 77.6.5 Preocupado el administrador por los primeros resultados, ahora desea conocer si el puntaje medio es menor a 7.
wilcox.test(x, mu=7, alternative = "l", exact = FALSE )##
## Wilcoxon signed rank test with continuity
## correction
##
## data: x
## V = 40, p-value = 2e-04
## alternative hypothesis: true location is less than 77.7 Test pareado de T-test
Cuando la toma de muestras no es independiente, se recomienda el test pareado. Esto es cuando la muestra de un evento es medida en dos tiempos diferentes, y cuando se les aplica a una población o muestra algún sistema o tratamiento.
No es necesaria la homogeneidad de las varianzas, ni que las muestras sean extraídas de la misma población.
La hipótesis nula es: los signos se distribuyen al azar alrededor de la mediana.
La aplicación en R es la misma al t-test, excepto que hay que especificar paired=T, indicando que se quiere un test pareado, de otra manera paired=F, se obtiene el t de student, no pareado.
7.7.1 Se desarrolla una investigacion para conocer el efecto placebo en pacientes con cierto tipo de enfermedad. Se mide una cierta determinacion medica en un tiempo uno (t1: sin tomar el placebo) y su respuesta en un tiempo dos (t2: despues de haber tomado el placebo), para conocer si hubo un efecto. Los pacientes desconocen que el medicamento es un simple placebo. Los datos son los siguientes:**
t1<-c(23,34,26,36,17,37,24,26,19,24,29,29)
t2<-c(25,37,27,33,22,36,30,30,25,29,32,34)Para ver mejor nuestros datos realizamos un único boxplot que contenga la unión de nuestros datos.
cbind(t1,t2)->tp
boxplot(tp,col=c("wheat3","skyblue4"),main="Boxplot\nEfecto Placebo")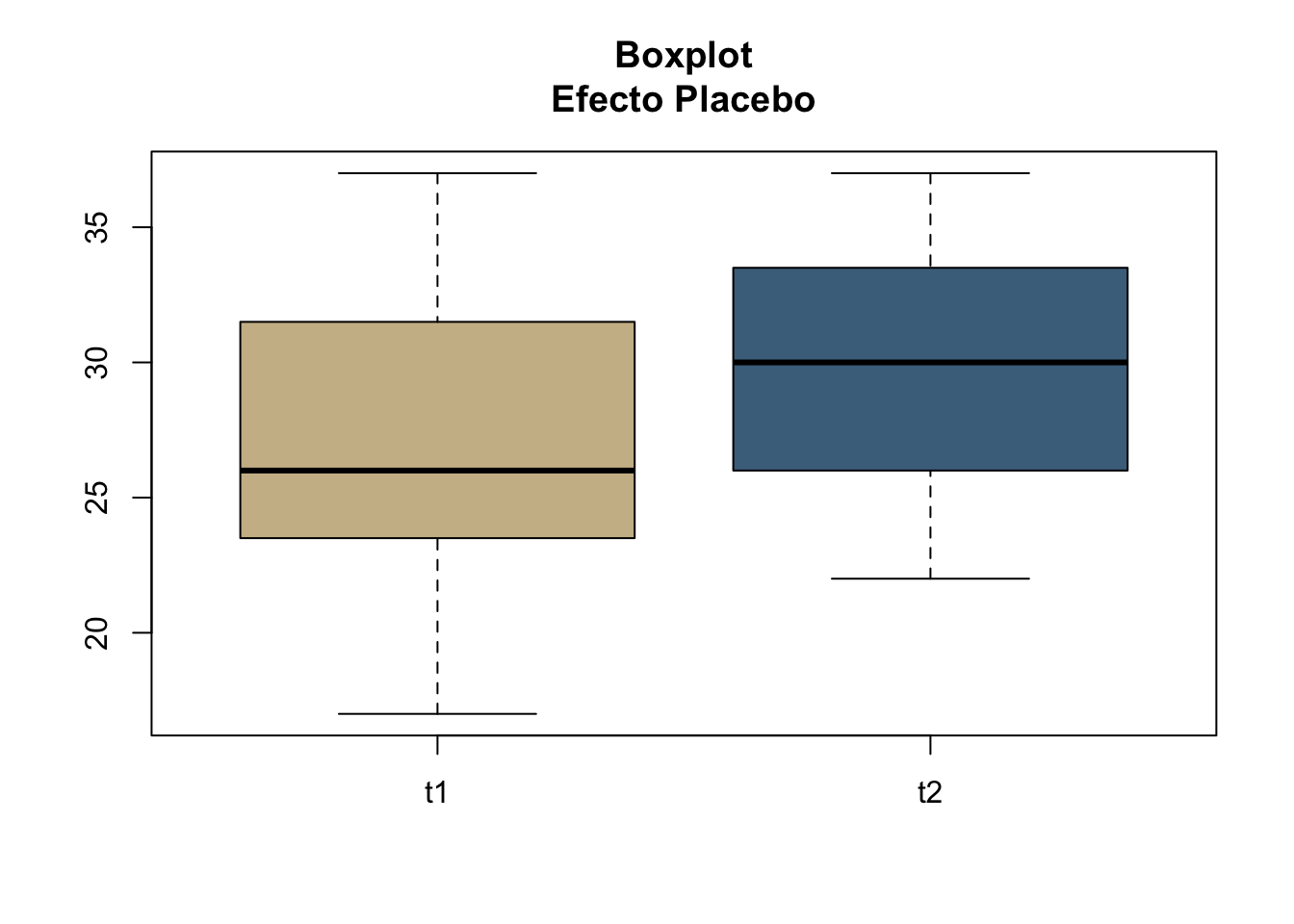
Figura 7.5: Boxplot del efecto placebo en t1 y t2.
R/ existe un efecto placebo de manera significativa entre los pacientes (t=-3.67; gl=11,p.value<0.05).
7.8 Test pareado de Wilcoxon
Es similar al test de una muestra de Wilcoxon, y análogo al t-test, y trabaja elaborando rangos para el calculo de p.value (Dalggard, 2002). Pertenece al grupo de las pruebas no paramétrica.
7.8.1 Se evalua la reduccion del peso (Kg) en personas obesas luego de seguir un regimen de dieta y ejercicios. Se les tomo el peso inicial (p1), y tres meses despues el peso final (p2). Los datos son los siguientes:**
P1<-c(111,128,111,117,119,90,115,118,109,115,118,113,92,79,75,93,86,99,118)
P2<-c(88,118,100,107,119,87,105,121,111,117,108,103,96,82,72,90,91,92,115)7.8.2 Se desea conocer si el régimen medio de la dieta fue efectivo?
Solución.
Importante siempre verificar el supuesto de normalidad
shapiro.test(P1)##
## Shapiro-Wilk normality test
##
## data: P1
## W = 0.9, p-value = 0.04shapiro.test(P2)##
## Shapiro-Wilk normality test
##
## data: P2
## W = 1, p-value = 0.5data.frame(P1,P2)->rd
rd #hay 19 pares de observaciones (util para obtener los gl)## P1 P2
## 1 111 88
## 2 128 118
## 3 111 100
## 4 117 107
## 5 119 119
## 6 90 87
## 7 115 105
## 8 118 121
## 9 109 111
## 10 115 117
## 11 118 108
## 12 113 103
## 13 92 96
## 14 79 82
## 15 75 72
## 16 93 90
## 17 86 91
## 18 99 92
## 19 118 115boxplot(rd,col="gray85", main="Boxplot\nRegimen de Dieta")
wilcox.test(P1,P2, paired=T,conf.int = TRUE, exact = FALSE)##
## Wilcoxon signed rank test with continuity
## correction
##
## data: P1 and P2
## V = 100, p-value = 0.02
## alternative hypothesis: true location shift is not equal to 0
## 95 percent confidence interval:
## 0.5 8.5
## sample estimates:
## (pseudo)median
## 4R/ el régimen de dieta aplicado a las personas resulto ser efectivo (Wilcox=138; gl=17;p-value=0.02).
Nota: Observe que los grados de libertad salen de pares de observaciones menos 2.
7.9 Comparacion de las varianzas para dos poblaciones o grupos
En R es posible obtener la comparación de varianza a través de la prueba de dos muestras t.test.
La hipótesis establecida asume que las varianzas son iguales en los dos grupos.
Utilizaremos los datos del ejemplo 7.6.
var.test(P1,P2)##
## F test to compare two variances
##
## data: P1 and P2
## F = 1, num df = 20, denom df = 20, p-value = 0.7
## alternative hypothesis: true ratio of variances is not equal to 1
## 95 percent confidence interval:
## 0.457 3.082
## sample estimates:
## ratio of variances
## 1.19R/ los dos grupos presentan varianzas iguales.
var.test(t1,t2)##
## F test to compare two variances
##
## data: t1 and t2
## F = 2, num df = 10, denom df = 10, p-value = 0.3
## alternative hypothesis: true ratio of variances is not equal to 1
## 95 percent confidence interval:
## 0.53 6.39
## sample estimates:
## ratio of variances
## 1.84R/ los dos grupos presentan varianzas iguales.
Para comparar varianzas de dos o mas grupos, también puede realizar a través de Bartlett’s o Levene’s test, que serán desarrollados en los próximos capítulos.
7.10 Kolmogorov-Smirnov test
Este es otro tipo de prueba que se utiliza para comparar la normalidad de un conjunto de datos. La prueba determina si los datos provienen de una misma distribución. Puede ser utilizado también para comparar si un conjunto de datos se ajustan a una distribución (en nuestro caso normal).
Cuando las muestras son pequeñas la prueba de Kolmogorov es una prueba menos poderosa para detectar diferencias significativas.
Respecto a la prueba de normalidad de Shapiro, esta resulta ser mas sensitiva que Kolmogorov. Es probable que la primera muestre que no existe normalidad y la segunda que si. Veamos una comparación de resultados según la prueba de Datos ejemplo 7.7
shapiro.test(P1)##
## Shapiro-Wilk normality test
##
## data: P1
## W = 0.9, p-value = 0.04mean<-mean(P1)
sd<-sd(P1)
ks.test(P1, "pnorm", mean=mean(P1), sd=sd(P1))## Warning in ks.test(P1, "pnorm", mean = mean(P1), sd =
## sd(P1)): ties should not be present for the Kolmogorov-
## Smirnov test##
## One-sample Kolmogorov-Smirnov test
##
## data: P1
## D = 0.2, p-value = 0.3
## alternative hypothesis: two-sidedComo observa, en este caso Shapiro muestra que no existe normalidad de datos (P1), mientras que Kolmogorov si lo muestra, en el mismo vector, demostrando así la sensibilidad de cada una de las pruebas.
Para aplicar la prueba de Kolmogorov, trabajaremos siempre con los datos del ejemplo 7.7.
ks.test(P1,P2)## Warning in ks.test(P1, P2): cannot compute exact p-
## value with ties##
## Two-sample Kolmogorov-Smirnov test
##
## data: P1 and P2
## D = 0.3, p-value = 0.3
## alternative hypothesis: two-sidedLos datos presentan normalidad. Recuerde siempre visualizar de forma gráfica los datos.
plot(ecdf(P1),xlim=range(c(P1,P2)),main="Distribucion Empirica Acumulada\n(P1,P2)")
plot(ecdf(P2), add=TRUE, lty="dashed", col="red")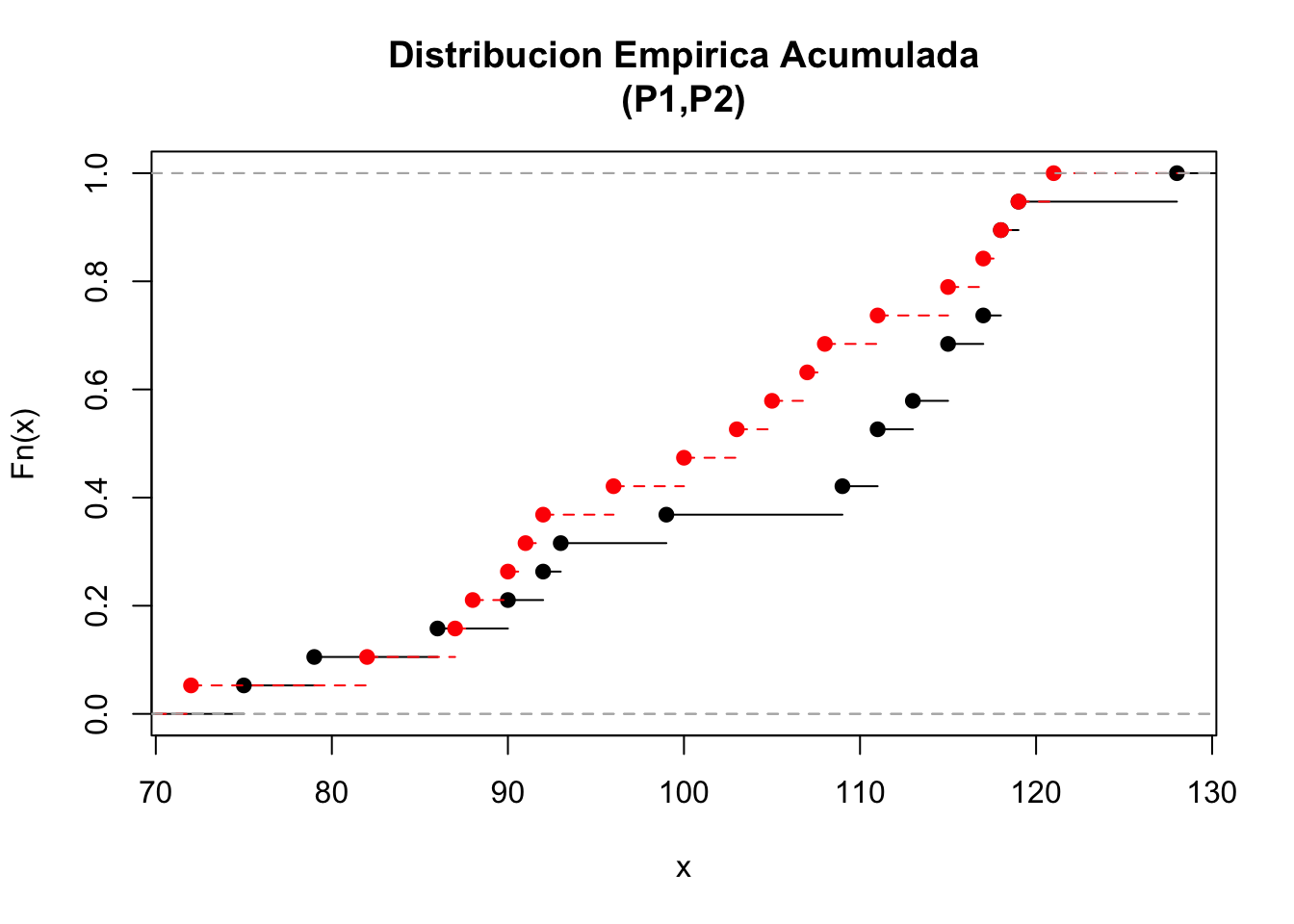
Figura 7.6: Distribución empírica acumulada para los vectores P1 y P2
qqplot(P1,P2, main="Q-Q Plot de P1 y P2")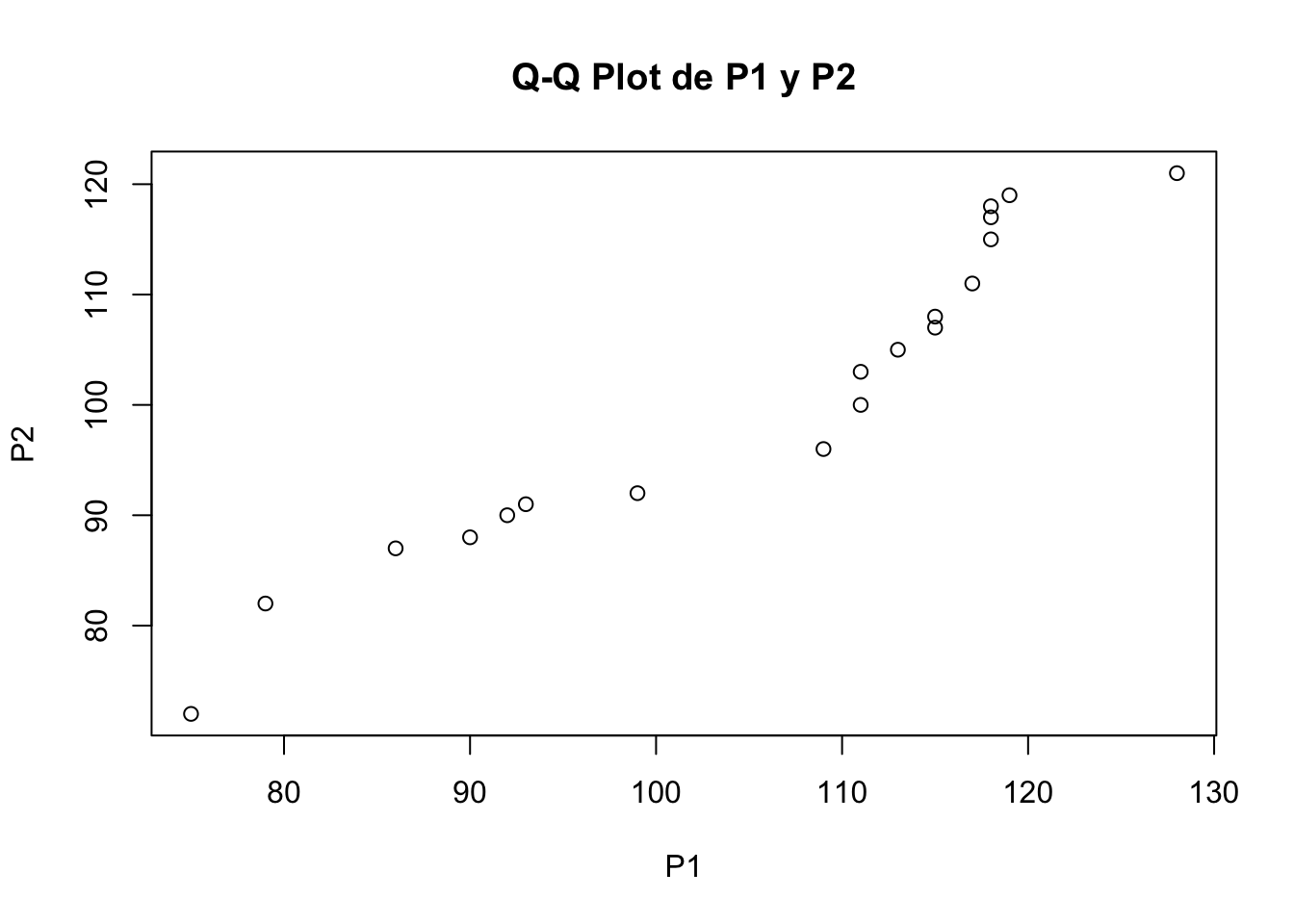
Figura 7.7: Q-Q plot para los vectores P1 y P2.
-qqplot-es la función para el trazado de los cuantiles una muestra contra los cuantiles de la muestra de otra muestra.
La normalidad es un supuesto que ciertas pruebas lo requieren, por eso es que se puede recurrir a la transformación de datos cuando el supuesto no se cumple (mas adelante se mostrará como ejecutarlo) cuando queremos ajustar esos valores.
7.11 Transformando datos
Muchos eventos en no se comportan de manera lineal (o no asumen una distribución normal), por lo que ocasionalmente se pueden utilizar transformaciones estadísticas (Logan, 2010). Una transformación en lo que incide, es tratar de estabilizar la varianza, o normalizar los datos. Algunos tipos mas comunes de transformación son:
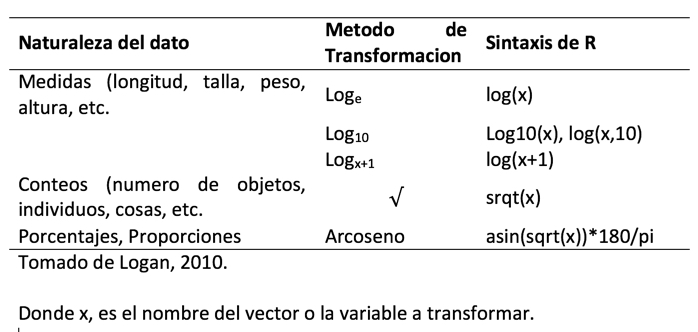
alt text
Siguiendo con los datos del ejemplo 7.7.
7.12 Transformacion Logaritmica.
qqplot(log(P1),log(P2), main="Q-Q Plot de log(P1) y log(P2)")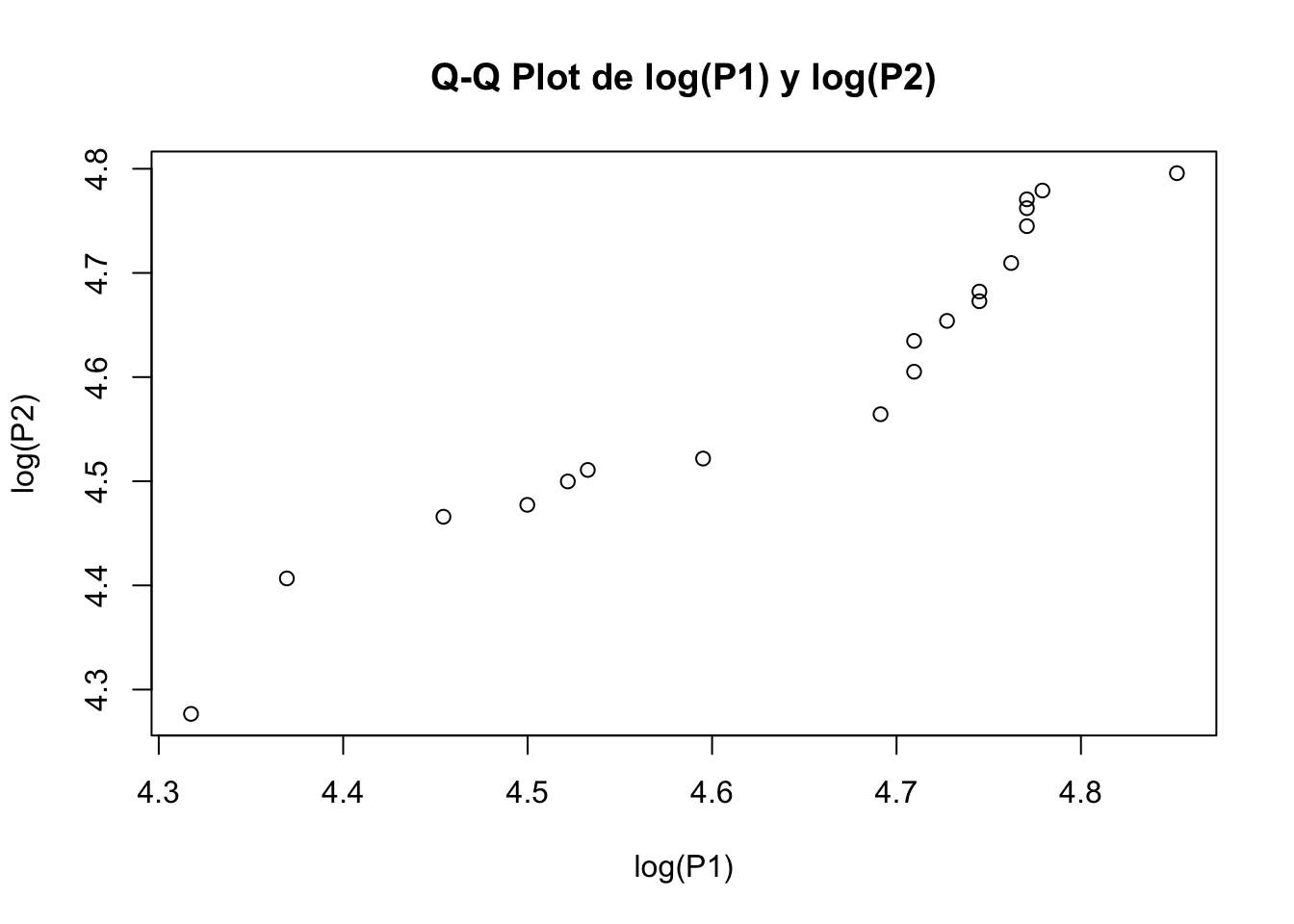
Figura 7.8: Cuantil Cuantil plot
7.13 Transformacion raiz cuadrada
qqplot(sqrt(P1),sqrt(P2), main="Q-Q Plot de sqrt(P1) y sqrt(P2)")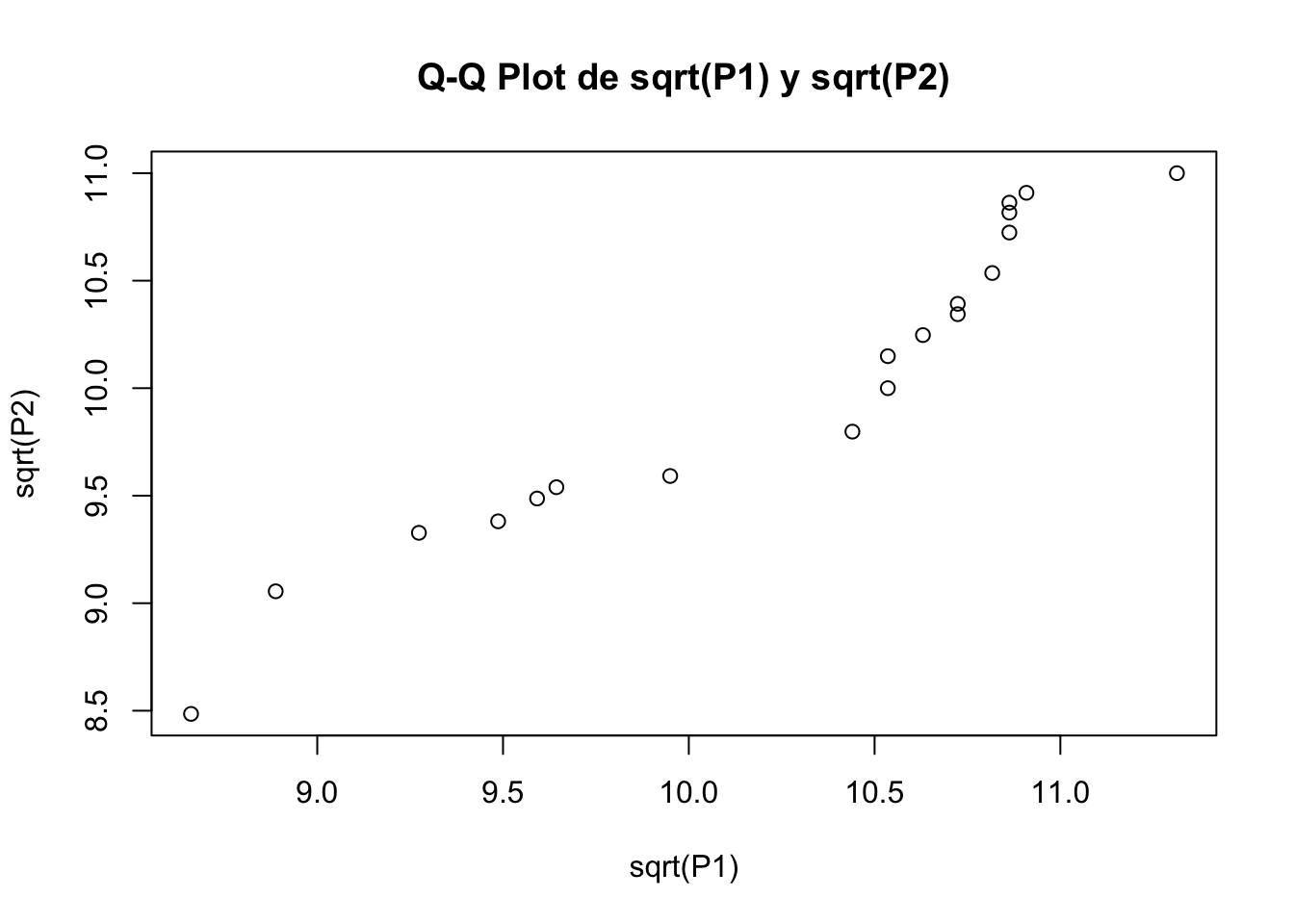
Figura 7.9: Q-Q plot de transformación logarítmica y raíz cuadra para el vector P1.
7.14 Test para dos muestras
A. partir de Poblaciones con Distribución Normal: Se Desconoce Las Varianzas de las Poblaciones, pero supone que son iguales
Trabaja el igual que la prueba de t-test. La diferencia es que analiza dos grupos. En este tipo de análisis podemos agruparlos en:
-Requiere de distribución normal, varianza desconocida
El estadístico de prueba es:
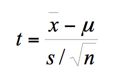
alt text
7.14.1 Se tiene dos grupos experimentales, donde se seleccionan al azar 25 muestras de cada grupo. Se mide en cada grupo una variable aleatoria x, y se obtiene que la media del primer grupo es de 25.6 con una desviacion estandar de 4.4. El grupo dos presento una media de 22.5, con una desviacion estandar de 2.98. **
7.14.2 Se quiere determinar si existe diferencia en los grupos experimentales, al 95% de confianza.**
set.seed(12345)
rnorm(25,mean=25.6, sd=4.4)->g1
set.seed(12345)
rnorm(25,mean=22.5, sd=2.98)->g2shapiro.test(g1)##
## Shapiro-Wilk normality test
##
## data: g1
## W = 1, p-value = 0.8shapiro.test(g2)##
## Shapiro-Wilk normality test
##
## data: g2
## W = 1, p-value = 0.8Se recomienda visualizar la normalidad de los datos utilizando qqnorm. Esta función le permite realizar una plot de probabilidad normal, que calcula los cuantiles de muestra contra los cuantiles teóricos. Si los puntos se distribuyen de forma simétrica, entonces los puntos se dispersan en torno a una linea recta.
par(mfrow=c(1,2))
qqnorm(g1); text(-1,23,"Grupo\ng1", col="red",font=8)
qqline(g1)
qqnorm(g2);text(-1,23,"Grupo\ng2", col="red",font=8)
qqline(g2)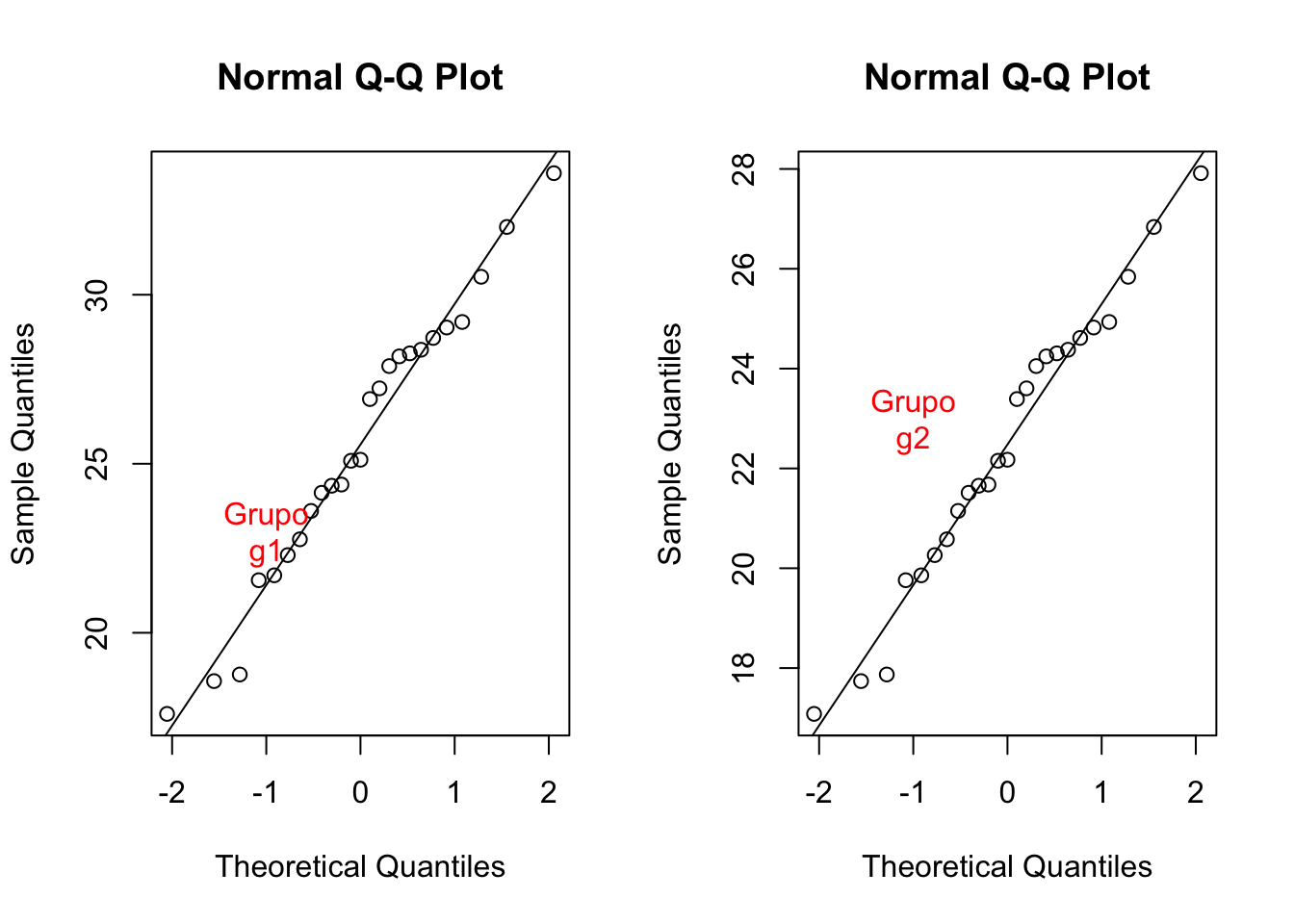
Figura 7.10: Cuantil-cuantil (Q-Q plot) de los datos g1 y g1.
7.14.3 Probar si las varianzas son iguales
var.test(g1,g2)##
## F test to compare two variances
##
## data: g1 and g2
## F = 2, num df = 20, denom df = 20, p-value =
## 0.06
## alternative hypothesis: true ratio of variances is not equal to 1
## 95 percent confidence interval:
## 0.961 4.947
## sample estimates:
## ratio of variances
## 2.18Nuestros datos presentan una distribución normal, varianzas desconocidas, pero suponen son iguales.
t.test (g1,g2,var.equal = T)##
## Two Sample t-test
##
## data: g1 and g2
## t = 3, df = 50, p-value = 0.003
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
## 1.08 5.12
## sample estimates:
## mean of x mean of y
## 25.6 22.5-Visualice un boxplot de las dos variables.
R/ Se encontró que existe una diferencia significativa entre los dos grupos experimentales de manera significativa (t=4.29; gl=48;p-value<0.05)
7.14.4 A partir de Poblaciones con Distribucion Normal: Se Desconoce Las Varianzas de las Poblaciones, pero supone que son desiguales.**
En este caso el test de Welch es el recomendado para prueba de hipótesis, estimación de intervalos de confianza y estimación de la media.
7.14.5 Se compara la edad de estudiantes que cursan el ultimo ano de colegio. El grupo 1, se trata de un colegio diurno y el grupo 2 de un colegio nocturno.**
Los datos son los siguientes.
edad1<-c(21.2, 23.8, 21.6, 23.0, 22.4, 22.8, 24.4, 21.7, 24.2, 21.7, 24.8, 22.4, 23.6, 23.2, 23.5, 22.4, 23.4, 23.7, 23.6, 23.5, 24.0, 24.3, 24.7, 24.3)
edad2<-c(24.1, 32.5, 34.8, 23.6, 24.3, 19.5, 26.1, 28.3, 19.8, 23.9, 19.0, 21.6, 29.0, 17.7, 29.0, 19.6, 26.5, 20.9, 19.9, 23.8, 19.1, 39.2, 29.2, 22.8)7.14.6 Se desea conocer si las edades medias de los grupos son diferentes.**
Recuerda siempre correr los supuestos de normalidad y homogeneidad de varianzas.
shapiro.test(edad1)##
## Shapiro-Wilk normality test
##
## data: edad1
## W = 0.9, p-value = 0.2shapiro.test(edad2) ##
## Shapiro-Wilk normality test
##
## data: edad2
## W = 0.9, p-value = 0.05var.test(edad1,edad2)##
## F test to compare two variances
##
## data: edad1 and edad2
## F = 0.04, num df = 20, denom df = 20, p-value =
## 1e-11
## alternative hypothesis: true ratio of variances is not equal to 1
## 95 percent confidence interval:
## 0.0153 0.0820
## sample estimates:
## ratio of variances
## 0.0355t.test(edad1,edad2,var.equal=F)##
## Welch Two Sample t-test
##
## data: edad1 and edad2
## t = -1, df = 20, p-value = 0.2
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
## -3.849 0.849
## sample estimates:
## mean of x mean of y
## 23.3 24.8Note el test que se aplica ahora es el de Welch, que asume que las varianzas de los grupos son desiguales, y es independiente del tamaño de la muestra.
A partir de Poblaciones con Distribución asimétrica
El estadístico de prueba es el Wilcoxon-Mann conocido también como prueba de Whitney U test, o Mann-Whitney-Wilcoxon Test.
La prueba se usa cuando no se puede verificar la suposición de dos poblaciones normales con varianzas iguales.
Compara las muestras independientes cuando estas no siguen una distribución normal y estas pueden ser de tipo cuantitativo, ordinal o categórico. Resulta útil para encontrar si dos muestras independientes proceden de poblaciones simétricas que tienen la misma media o mediana.
7.14.7 Se desarrolla un experimento donde se desea conocer si un tipo de atrayente resulta ser mas efectivo para la atraccion de insectos, los datos son medidos cada hora y se contabiliza la cantidad de insectos que visitan los atrayentes. Se utiliza un atrayente natural, vrs uno artificial.**
Atrayente natural color ciruela (plum) 19,25,35,30,29,29,28,30,16,25,26,16,17,21,24,35
Atrayente artificial, color zumo dulce (honeydew) 9,30,3,30,19,29,28,3,6,30,17,18,2,23,19,3
an<-c(19,25,35,30,29,29,28,30,16,25,26,16,17,21,24,35)
ar<-c(9,30,3,30,19,29,28,3,6,30,17,18,2,23,19,3)
shapiro.test(an)##
## Shapiro-Wilk normality test
##
## data: an
## W = 0.9, p-value = 0.3shapiro.test(ar)##
## Shapiro-Wilk normality test
##
## data: ar
## W = 0.9, p-value = 0.02cbind(an,ar)->df
boxplot(df, col=c("plum3","honeydew2"),main="Boxplot\natrayentes")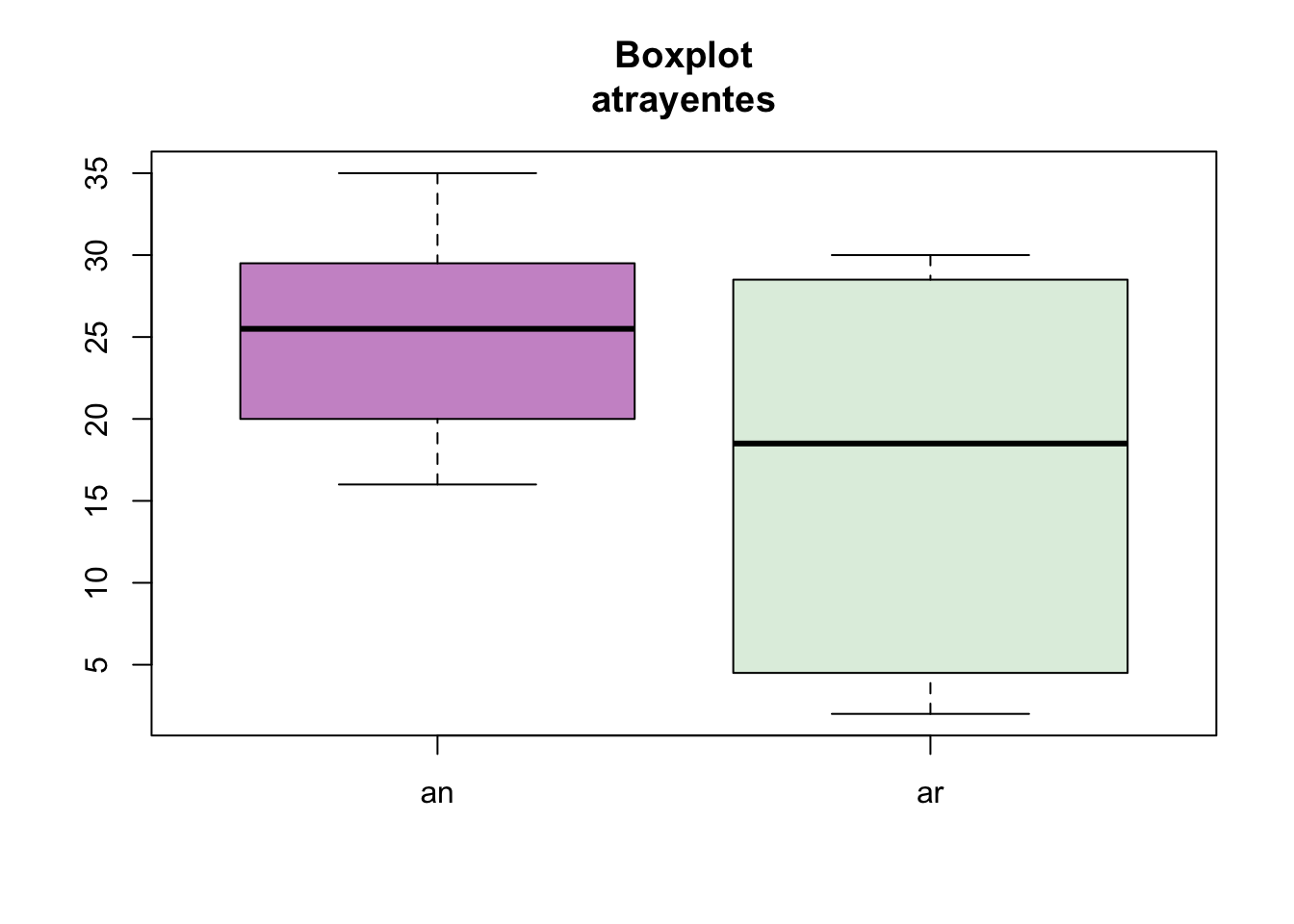
Figura 7.11: Boxplot de atrayente para las variables an y ar.
wilcox.test(an,ar, alternative = "g",correct=F)## Warning in wilcox.test.default(an, ar, alternative =
## "g", correct = F): cannot compute exact p-value with
## ties##
## Wilcoxon rank sum test
##
## data: an and ar
## W = 200, p-value = 0.03
## alternative hypothesis: true location shift is greater than 0diff<-c(an-ar)
diff## [1] 10 -5 32 0 10 0 0 27 10 -5 9 -2 15 -2 5 32R/ Se encontró que el atrayente natural resultó ser mas efectivo que el artificial de manera significativa (W=179; p-value=0.02).