Cap. 4 Aprendiendo Estadística

4.1 Métricas para estadísticas descriptivas

Uno de los principios en básicos para el entendimiento de situaciones y análisis, es la exploración básica de los datos. Para ello hay diversas formas de ejecutarlo.

Utilizaremos la base de datos “InsectSprays” de los set de datos de R. Ver cuadro

Cuadro 4.1: Visual de los primeros quince datos de InsectSprays
count	spray
10	A
7	A
20	A
14	A
14	A
12	A
10	A
23	A
17	A
20	A
14	A
13	A
11	B
17	B
21	B

Las métricas de la estadística descriptiva son útiles para entender la distribución de los datos. Con ello, podemos ver medidas de posición o tendencia central, medidas de dispersión, entre otras.

Algunas funciones para obtener resúmenes estadísticos pueden ser obtenidas utilizando los siguiente comando:

mean(): Promedio
sd(): Desviación estándar
median: Mediana
var(): Varianza
min(): Valor mínimo
min(): Valor mínimo
max(): Valor máximo
range(): Rango de valores
quantile(): Cuantiles y percentiles
IQR(): Rango intercuartílico

Las medidas de posición central son las que resumen en un solo valor un conjunto de valores. Éstas siempre van a representar un centro en el cual se encuentra un conjunto de datos.

Entre las medidas de posición central más utilizadas tenemos:

Promedio: Es la medida mas utilizada y se conoce también como la media aritmética o promedio aritmético. Y se estima como la sumatoria de todos los valores, dividido entre el número total de ellos. Hay que tener en cuenta que el promedio es sensitivo a los “outliers” (valores extremos).
Mediana: Es el valor que ocupa una posición central, en donde si se disponen los datos ordenados de forma ascendente, este siempre representa exactamente la mitad de los datos.
Moda:Es el valor mas frecuente entre mis datos.

Las medidas de dispersión más utilizadas son:

Desviación estándar: Se refiere a que tan dispersos están mis datos respecto al promedio de mis datos.
La Varianza: Corresponde al cuadrado de la desviación estándar.
El Coeficiente de Variación: Mide el porcentaje de variabilidad de los datos. Es útil para hacer referencia a la relación entre el tamaño de la media y la variabilidad de la variable. Siempre será expresado en porcentaje. A mayor porcentaje habrá una mayor variabilidad entre los datos.
El rango intercuartílico: conocido como IQR (por sus siglas en inglés), es la diferencia de los valores del tercer y del primer cuartil. Tiene la ventaja que excluye la mayoría de los valores atípicos.

El resumen estadístico a través de la función “summary()”, es el más clásico de los análisis exploratorios. Este nos indica las siguientes métricas estadísticas.

4.2 Resumenes de datos numéricos en R.

La forma mas sencilla de obtener un resumen de datos numéricos es a través de la función “summary”. Utilizaremos la base de datos “InsectSprays” de la base de datos de R.

data(InsectSprays) #permite cargar la base de datos
summary(InsectSprays)

##      count      spray 
##  Min.   : 0.0   A:12  
##  1st Qu.: 3.0   B:12  
##  Median : 7.0   C:12  
##  Mean   : 9.5   D:12  
##  3rd Qu.:14.2   E:12  
##  Max.   :26.0   F:12

Min.:Muestra los valores mínimos del conjunto de datos.
1st Qu.: Primer cuartil: Representa el 25% de los valores en el conjunto de datos de forma ascendente.
Median: Muestra la mediana de los datos.
Mean: Promedio.
3rd Qu.: Tercer cuartil.
Max.: Valor máximo.

Para entender mejor cada alguno de estos conceptos visualizaremos un diagrama de cajas. En él se distribuye cada una de las métricas descriptivas. Asocie cada valor del resumen estadístico en la figura .

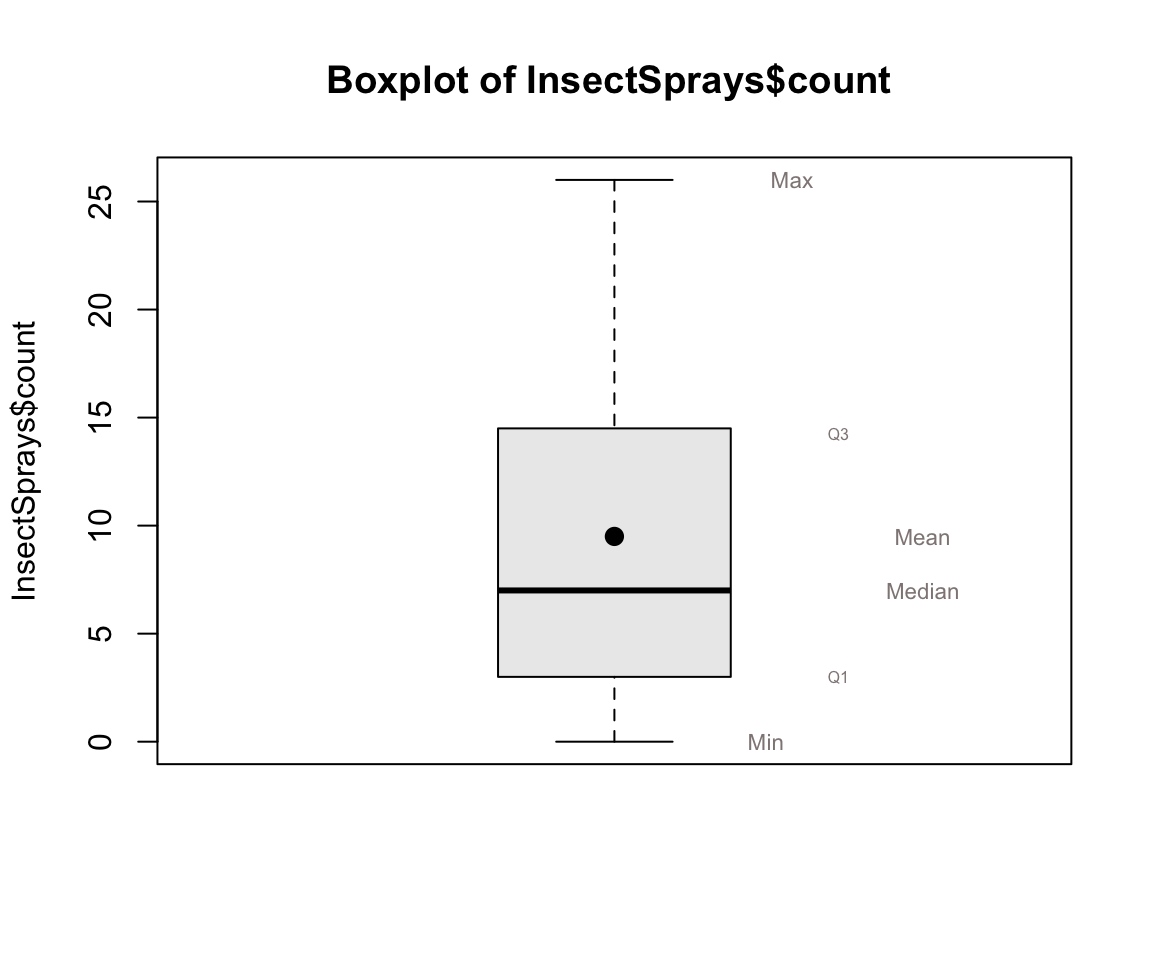
Figura 4.1: Diagrama de Cajas de InsectSprays para la variable count

Vamos a interpretar estos cálculos. Solicitar la ayuda de “?InsectSprays”, para entender de que tratan los datos. Ahí, se interpreta que tratan sobre la efectividad de un spray insecticida.

El valor mínimo indica la cantidad mas baja de insectos afectados.

El primer cuartil, que refiere al 25% de los datos ordenados en forma ascendente, tenemos que menos de 3 insectos fueron afectados.

La mediana o segundo cuartil, indica que menos de 7 insectos fueron afectados.

El tercer cuartil, que refiere al 75% de los datos ordenados en forma ascendente muestra que menos de 14.25 insectos fueron afectados.

El valor máximo indica la cantidad más alta de insectos afectados.

Si usted quiere ver los valores ordenados de forma ascendente, utilice la función “sort”.

sort(InsectSprays$count)

##  [1]  0  0  1  1  1  1  1  1  2  2  2  2  3  3  3  3  3
## [18]  3  3  3  4  4  4  4  5  5  5  5  5  5  5  6  6  6
## [35]  7  7  7  9 10 10 10 11 11 11 12 12 13 13 13 13 14
## [52] 14 14 14 15 15 16 16 17 17 17 17 19 20 20 21 21 22
## [69] 23 24 26 26

Contraste el resultados de los datos ordenador con la figura y trate de interpretar cada valor.

4.2.1 Estructura de los datos

Antes de empezar a correr cualquier análisis es importante entender la estructura de los datos. Esto nos va a permitir correr análisis estadísticos sin ningún inconveniente.

La función “str” permite ver la información o estructura de sus datos. Esto es útil cuando exportamos una base de datos y desconocemos el origen o contenido de cada variable.

str(InsectSprays)

## 'data.frame':    72 obs. of  2 variables:
##  $ count: num  10 7 20 14 14 12 10 23 17 20 ...
##  $ spray: Factor w/ 6 levels "A","B","C","D",..: 1 1 1 1 1 1 1 1 1 1 ...

Podemos observar que la variable “count” es numérica y la variable “spray” es un factor. Al ser una variable factor no podremos calcular estadísticas básicas como medidas de posición central o dispersión.

4.2.2 Cantidad de datos

Lo que nos permite esta función es contar la cantidad de valores asociados a un vector, entiéndase en el lenguaje de escritura para artículos se refiere al valor de n (cantidad de valores de muestra).

length(InsectSprays$count)

## [1] 72

4.2.3 Mediana

sort(InsectSprays$count)

##  [1]  0  0  1  1  1  1  1  1  2  2  2  2  3  3  3  3  3
## [18]  3  3  3  4  4  4  4  5  5  5  5  5  5  5  6  6  6
## [35]  7  7  7  9 10 10 10 11 11 11 12 12 13 13 13 13 14
## [52] 14 14 14 15 15 16 16 17 17 17 17 19 20 20 21 21 22
## [69] 23 24 26 26

median(InsectSprays$count)

## [1] 7

Para entender la mediana, vimos anteriormente que tenemos 72 valores. Si la cantidad de valores es par, la mediana siempre es el promedio de los dos números centrales, en nuestro caso: 72/2=36. Buscamos el valor de 36 en posición dentro de los valores y notamos que corresponde a los valores 7 y el siguiente valor en orden superior sería 7. Por lo que (7+7)/2=7.

Entiéndase de una forma mas simple. Cuando los valores son pares se seleccionan los valores centrales, estando los datos ordenados en forma ascendente, ejem.

#Supongase estos valores contenidos en el objeto a.
a<-c(1,2,3,4)
median(a)

## [1] 2.5

#A ellos se les suma los dos valores centrales (2+3) y siempre se dividen entre 2.

En caso que los valores sean impares

#Supongase estos valores contenidos en el objeto b.
b<-c(1,2,3,4,5)
#Se estima como n +1, dividido entre 2.
#que sería (5+1)/2.
median(b)

## [1] 3

4.2.4 Promedio

mean(InsectSprays$count)

## [1] 9.5

4.2.5 Valor máximo

max(InsectSprays$count)

## [1] 26

4.2.6 Valor mínimo

min(InsectSprays$count)

## [1] 0

4.2.7 Cuantiles, Cuartiles y Percentiles

Un cuantil divide una distribución de datos aleatoria en partes.

Los cuantiles más conocidos son:

Cuartiles: Dividen a la distribución en 4 partes: 0.25, 0.50 y 0.75
Deciles: Dividen a la distribución en las partes iguales, cada una de las cuales engloba el 10 % de los datos.
Percentiles: Dividen a la distribución en 100 partes iguales, cada una de las cuales engloba el 1 % de las observaciones.

quantile(InsectSprays$count)

##    0%   25%   50%   75%  100% 
##  0.00  3.00  7.00 14.25 26.00

4.2.8 Percentiles

De la misma forma para estimar cuantiles, puedo obtener los percentiles

#Percentil 10
quantile(InsectSprays$count,.10)

## 10% 
## 1.1

#Percentil 90
quantile(InsectSprays$count,.90)

## 90% 
##  20

Hay algunas métricas de gran utilidad que R no las brinda, por lo que hay que ayudarse instalando paquetes adicionales para obtener una estadística de interés, ejem. el error estándar y coeficiente de variación.

\(~\) \(~\)

Nota:

Recuerde instalar los paquetes en caso de no tenerlos instalados en su computador

Utilizaremos el paquetes “resumeRdesc” para obtener estadísticas descriptivas de una formas mas rápida.

Un paquete estadístico, que propone no solo brindar resultados, si no que tiene la novedad de brindar interpretaciones de texto de sus resultados.

El paquete de resumeRdesc fue construido con el fin de ayudar a estudiantes, investigadores y todas aquellas personas que viven haciendo análisis continuo descriptivo en en el software de R. Bajo la necesidad de responder a estos grupos de interés, y de conocer las métricas descriptivas más usadas para sus datos, resumeRdesc viene a dar respuestas de una forma fácil, rápida y sencilla.

La función resume, le permite realizar una inspección visual del comportamiento de sus datos.

En la parte de resultados podrá leer:

Si sus datos presentan una distribución normal.
Si su tamaño de muestra es bueno (esto basado en el concepto estadístico arbitrario de n>=30).
Le permite conocer si sus datos presentan valores “outlier”.

La ventana gráfica le permite inspeccionar tres tipos de figuras:

Histograma y densidad: Le permite reconocer la tendencia y simetría de sus datos. Así mismo, se muestra el valor de la media y mediana de la población.
Diagrama de cajas: le permite ver la distribución de sus datos, y se le adiciona la posición de la referencia de la media de sus observaciones.
Quantile-quantile plot: Le permite ver el ajuste de la simetría de sus datos, para confirmar si la distribución simétrica se cumple.

En la misma ventana gráfica se adiciona un recuadro de estadísticas descriptivas,que incluyen:

el tamaño de la muestra “n”
mean: el promedio
sd: la desviación estándar
Median: la mediana
Max: el valor máximo
Min: el valor mínimo
Confident.Intervals: Intervalo de confianza al 95%
Shapiro-Wilk test: test de la distribución normal de Shapiro
Distr: Indicación de su si distribución de datos es o no simétrica
Sample size: indicación basada en el tamaño de la muestra.

set.seed(12345) #Permite establecer una semilla de datos
data<-rnorm(100) #Genera 100 datos con una distribución normal
resume(data)

## [1] "You got Normal distribution."
## [1] "You got a good sample size (n>=30)"
## [1] "You do not have outlier"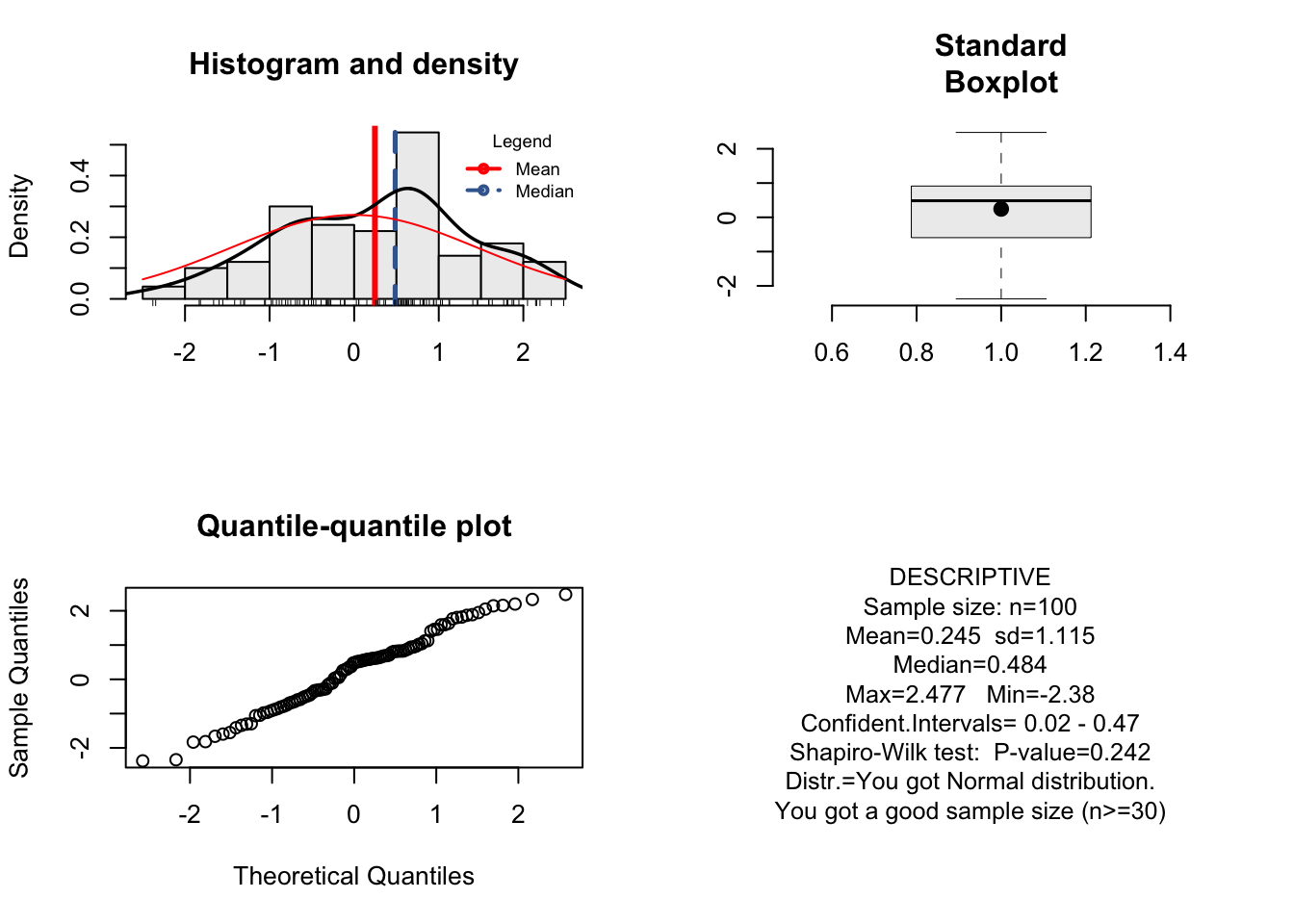

4.3 Resumen completo.

La función resume2data, le permite obtener un resumen completo de las estadísticas descriptivas. Así mismo, se podrá visualizar un histograma y diagrama de cajas basado en la distribución de sus datos.

set.seed(12345) #Permite establecer una semilla de datos
data<-rnorm(100) #Genera 100 datos con una distribución normal
resume2data(data)

## This function shows summary statistics.
##                   It includes measures of central tendency,
##                   measures of variability,
##                   and measures of shape.

## [[1]]
## NULL
## 
## [[2]]
##                Size (n)                 Missing 
##               100.00000                 0.00000 
##                 Minimum                  1st Qu 
##                -2.38000                -0.59000 
##                  Median                  3st Qu 
##                 0.48400                 0.90000 
##                     Max                    Mean 
##                 2.47700                 0.24500 
##                      sd                     Var 
##                 1.11500                 1.24300 
##                 SE Mean                  TrMean 
##                 0.11200                 0.25800 
##                     IQR                   Range 
##                 1.49000                 4.85700 
##                Kurtosis                Skewness 
##                 2.44000                -0.14000 
##                      CV                 CI.Mean 
##                 4.55102                 0.00704 
##                  lwr.ci                  upr.ci 
##                 0.02000                 0.47000 
##                     Sum      Shapiro.test p-val 
##                24.51972                 0.24200

4.3.1 Resumenes para marcos de datos (data.frame)

La función resumendf, le permite obtener métricas basadas en una estructura de datos en “data.frame”.

Las métricas que se pueden obtener son:

“n”: el tamaño de la muestra
“Mean”: el promedio
“sd”: la desviación estándar
“Median”: la mediana
“Min”: el valor mínimo
“Max”: el valor máximo
“1st Qu”:el primer cuartil
“3st Qu”:el tercer cuartil
“se”: el error estándar
“Missing”: valores faltantes

Así mismo, se brinda un boxplot entre los grupos existentes de su “data.frame”. Para ilustrar usaremos la base de datos denominada “iris”.

data(iris)
resumendf(Petal.Width ~Species, data = iris)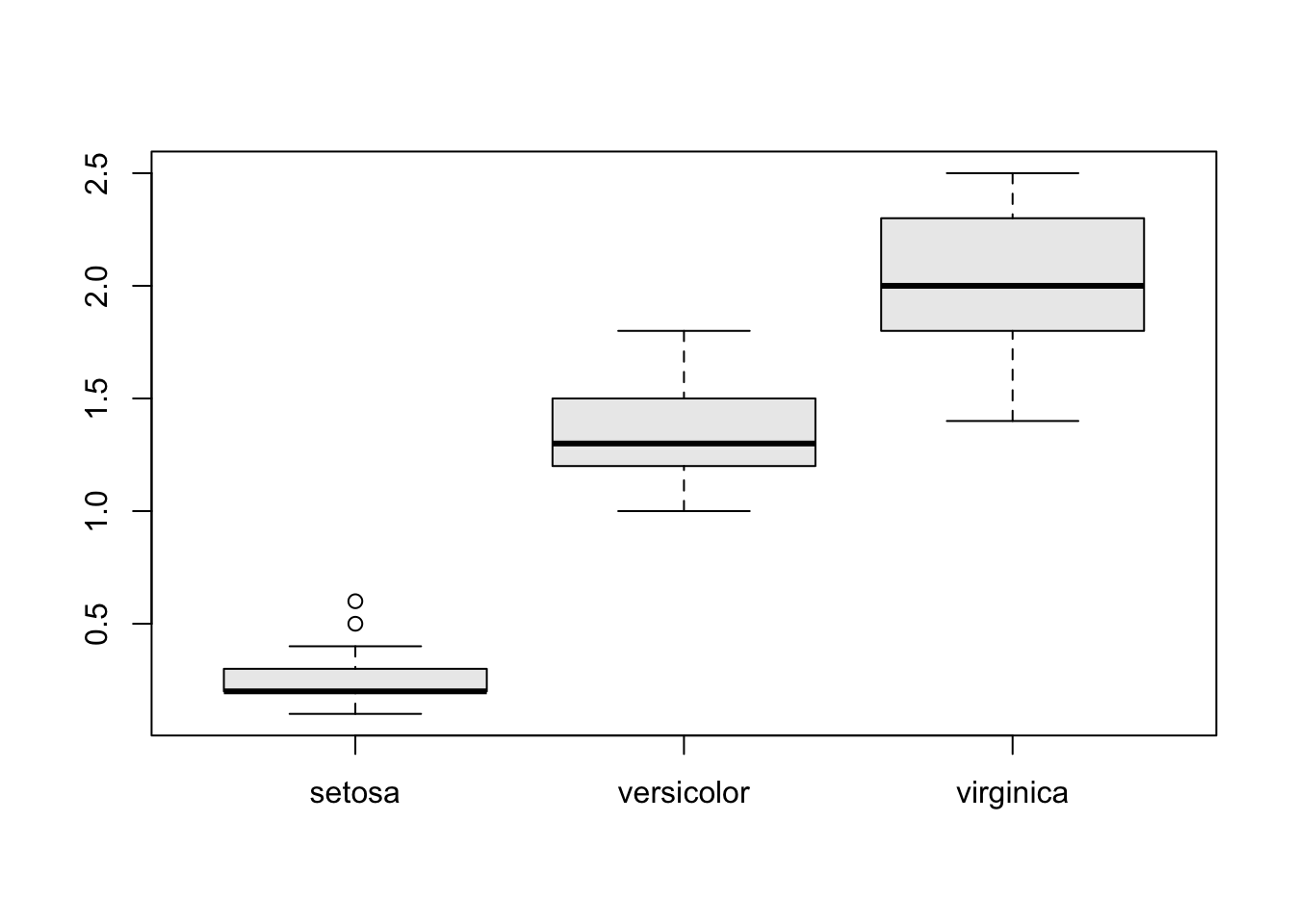

##             n  Mean    sd Median Min Max 1st Qu
## setosa     50 0.246 0.105    0.2 0.1 0.6    0.2
## versicolor 50 1.326 0.198    1.3 1.0 1.8    1.2
## virginica  50 2.026 0.275    2.0 1.4 2.5    1.8
##            3st Qu     se Missing
## setosa         0.3 0.015       0
## versicolor     1.5 0.028       0
## virginica      2.3 0.039       0

Otras métricas que se pueden obtener utilizando el paquete de “resumeRdesc” son:

4.4 Coeficiente de variación

Mide el porcentaje de variabilidad de los datos.

datos<-c(1,2,3,4,5,6,7,8,9,10)
cv(datos)

## [1] 0.55

4.5 Media Geométrica

La media geométrica es una media o promedio, y lo que indica es una tendencia central de los datos.

datos<-c(1,2,3,4,5,6,7,8,9,10)
g_mean(datos)

## [1] 4.53

4.6 Media Armónica

La media armónica es un tipo de promedio muy específico. Generalmente se usa cuando se trata de promedios de unidades, como la velocidad u otras tasas y proporciones. Es un recíproco de los números en su conjunto de datos o se calcula dividiendo el número de observaciones por el recíproco de cada número en la serie.

datos<-c(1,2,3,4,5,6,7,8,9,10)
h_mean(datos)

## [1] 3.41

4.7 Moda

La “Moda” se entiende como el dato mas frecuente entre mis datos

data2<-c(1,1,1,2,3,4,4,4,4,5,6,7,8,9)
Mode(data2)

## [1] 4

En nuestro caso el valor mas frecuente sería el valor de 4.

Otra forma de obtener la moda es a través del comando “table”.

data2<-c(1,1,1,2,3,4,4,4,4,5,6,7,8,9)
table(data2)

## data2
## 1 2 3 4 5 6 7 8 9 
## 3 1 1 4 1 1 1 1 1

El comando “table”, lo que hace es, contar la frecuencia de valores que se identifican con un cierto valor, en nuestro caso tenemos 3 veces el valor de uno, 1 vez el valor de 2, una vez el valor de 3, 4 veces el valor de 4 y así sucesivamente, hasta encontrar el que se repita mas veces, cuando la moda existe. No todos los valores siempre tendrá moda. En algunas ocasiones podrá ser bimodal.

data3<-c(1,1,1,2,3,4,4,4,5,5,6,7,8,9)
Mode(data3)

## [1] 1 4

En los caso que la moda aparezca en más de dos ocasiones, se convierte en una distribución multimodal.

data4<-c(1,1,1,2,3,4,4,4,5,5,5,6,7,8,9)
Mode(data4)

## [1] 1 4 5

4.8 Error estándar

Es como una medida de la precisión de la media de la muestra, y es considera como una medida de dispersión respecto a la media de los valores.

datos<-c(1,2,3,4,5,6,7,8,9,10)
se(datos)

## [1] 0.958

## mean= 5.5±0.958 =standard error

4.9 Curtosis

La curtosis se refiere a que sus datos, se acerca a una distribución normal. Si sus valores son cercanos a cero, presentan una distribución normal y si son alejados de cero no están distribuidos normalmente.

K(datos)

## [1] 1.78

4.10 Asimetría

La asimetría se refiere al grado en que los datos son asimétricos. A medida que los datos se vuelven simétricos, el valor se acerca a cero. La asimetría se denota como “g”.

g=0: La distribución es simétrica.
g>0: La curva es asimétrica positiva.
g1<0: La curva es asimétrica negativa.

skew(datos)

## [1] 0