Cap. 8 Distribución Normal Estándar

Este tipo de distribución se reconoce por su forma de campana, y resulta ser la distribución continua más importante, ya que mide en forma aproximada muchos fenómenos que ocurren en la naturaleza (Daniel, 2006; Logan, 2010).

La curva de distribución, se le llama campana de Gauss o gaussiana es asintótica, simétrica en ambos lados. Frecuentemente utilizada como modelo de datos continuos.

par(mfrow=c(2,2))

x<-seq(-3,3,length=100)
y<-dnorm(x)

Es así como se observa la distribución normal.

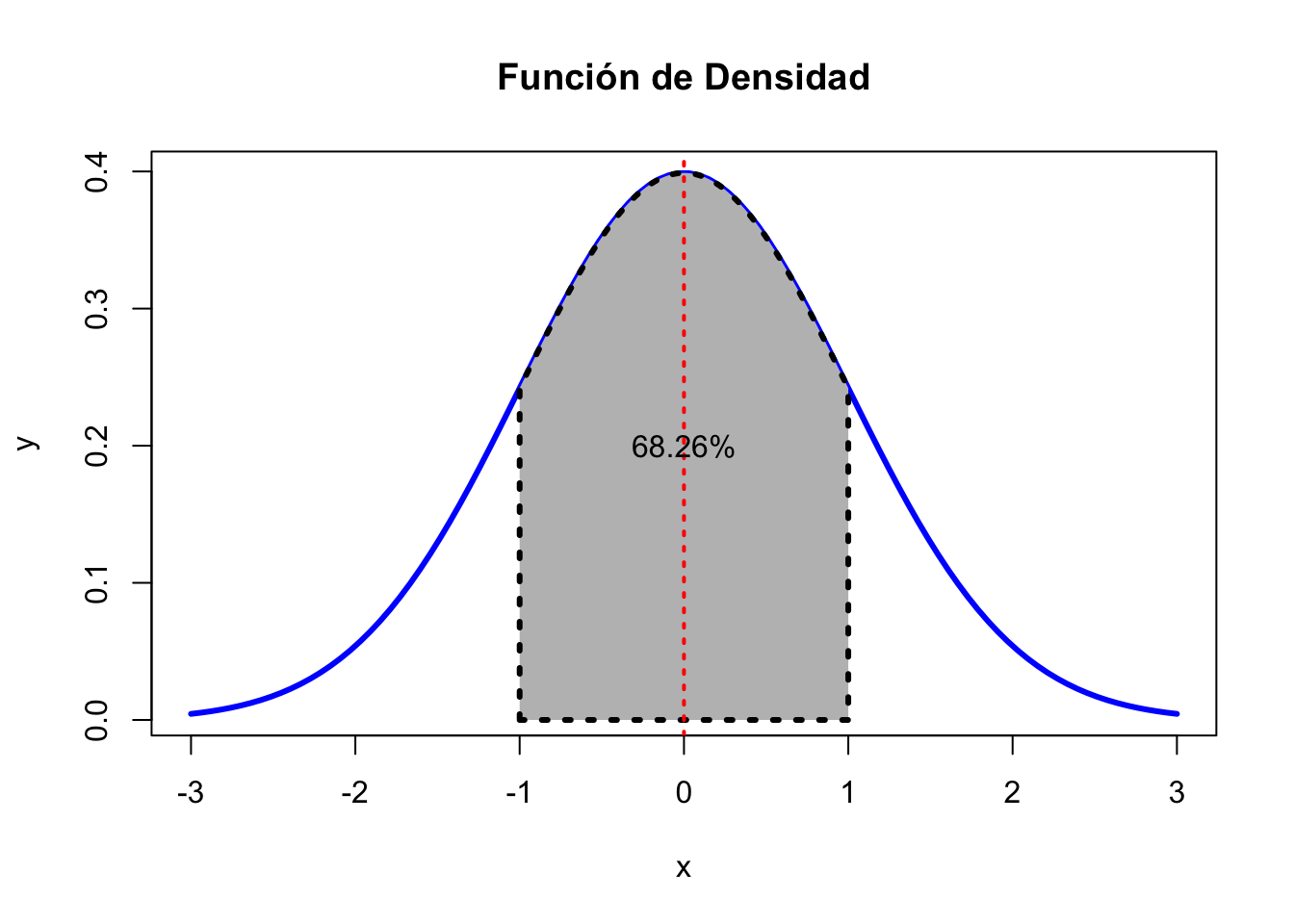
Figura 8.1: Función de densidad normal. El eje x etiqueta la distancia de las desviaciones estándares (sd) respecto a la media (mu=0).

Esto significa que alrededor del 68% de las observaciones extraídas aleatoriamente de una población distribuida normalmente, se encontrara dentro de los límites de 1 desviación típica alrededor de la media. El otro 32% estará fuera de estos valores (un 16% por encima de una desviación típica y el otro 16% por debajo). En otras palabras, la probabilidad de que una observación individual escogida al azar sea una descriptora de la población es de un 68% (Fowler, 1999).

La distribución normal está determinada por dos constantes: (media poblacional) que es igual a cero y (la desviación típica poblacional) que es igual a uno.

La función de densidad de la curva normal está dada por:

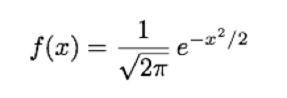
En R, otra forma de escribir esta función será:

x<-seq(-3,3,length=100)
y<-1/sqrt(2*pi)*exp(-x^2/2)
plot(x,y,type="l", lwd=3, col="blue", main="Función de Densidad")

La forma de cómo se construye una distribución continua con distribución normal, es utilizando los comandos: dnorm(), pnorm(), qnorm() y rnorm(). Para ver más detalles de la distribución solicite la ayuda.

? dnorm

La función dnorm() nos brinda los valores de probabilidad de la función de densidad.

La función pnorm() calcula la probabilidad acumulada, siendo esta el área bajo la curva hasta una ordenada (eje x) especifica.

pnorm(2, mean=0,sd=1)

## [1] 0.977

Para entender mejor en la forma gráfica proyectamos esta probabilidad.

x<-seq(-5,5,0.1)
hist <- dnorm(x, mean=0, sd=1) 
plot(x, hist, type="l", xlab="Desviación estándar", ylab="Densidad",main="Plot de Densidad", lty = 1, lwd = 3, yaxs="i") # yaxs="i" localiza en el eje el límite del dato
polygon(c(x[x <= 2.0], 2), c(dnorm(x[x <= 2]), 0), col="lightblue")
text(0, .1,"0.977")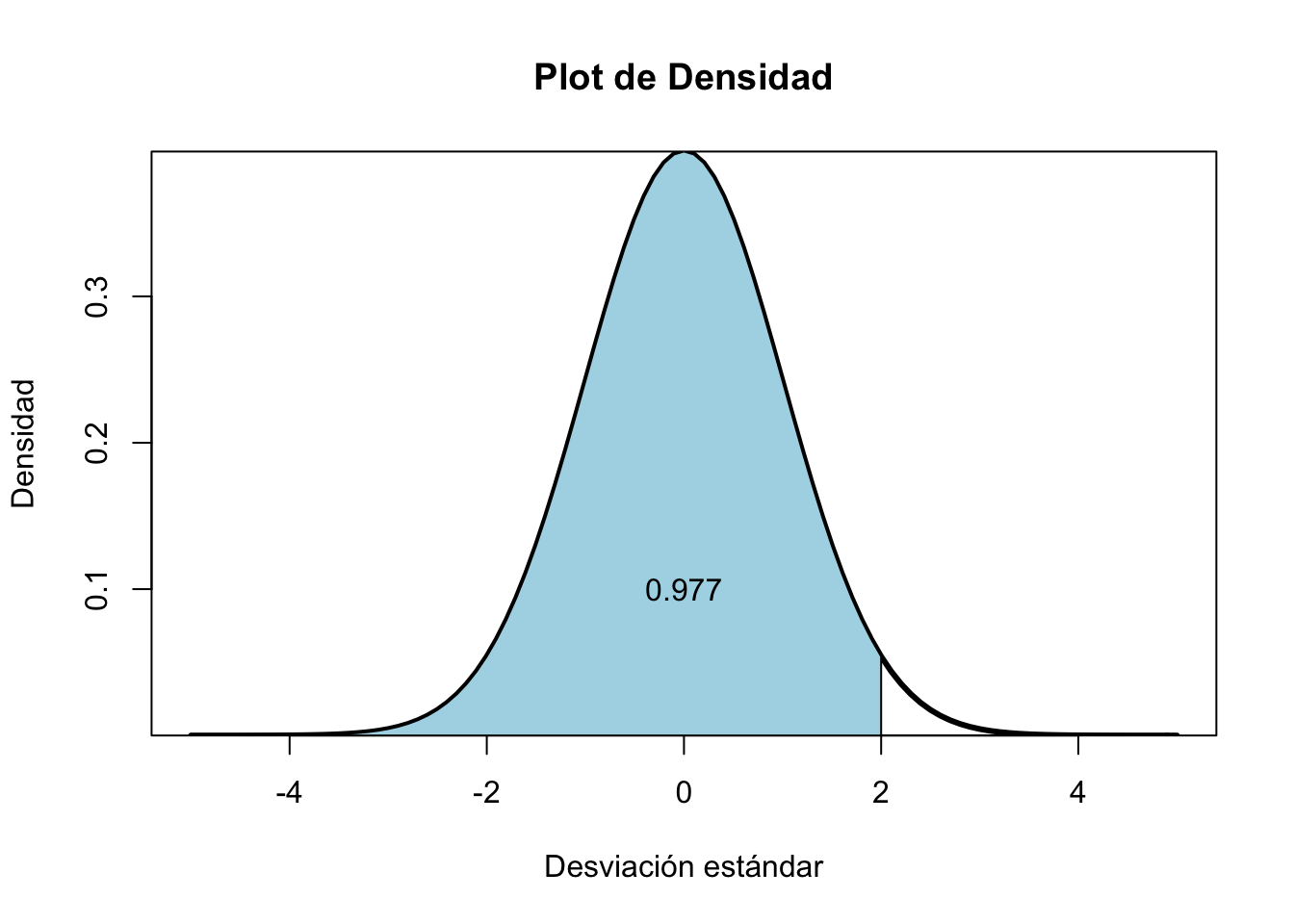

Figura 8.2: Función de distribución normal.

El área bajo la curva de la campana de Gauss (Figura. 2) en color celeste claro representa, que el 97.7% de desviaciones estándares normales son menores a 2 (100%). Bajo el supuesto que el área bajo la curva es 100% de una función de densidad.

La función qnorm(), determina el cuantil de una probabilidad dada.

qnorm( 0.9772499,mean=0, sd=1)

## [1] 2

El dato representa los valores menores asociados al percentil 97 de la distribución, con una media de cero y desviación estándar de uno.

rnorm(). Como hemos visto en las secciones anteriores, genera números aleatorios con distribución normal.

set.seed(12345) #vector integral que establece parámetros iguales para todas las computadoras.
rnorm(100,mean=0, sd=1)

##   [1]  0.5855  0.7095 -0.1093 -0.4535  0.6059 -1.8180
##   [7]  0.6301 -0.2762 -0.2842 -0.9193 -0.1162  1.8173
##  [13]  0.3706  0.5202 -0.7505  0.8169 -0.8864 -0.3316
##  [19]  1.1207  0.2987  0.7796  1.4558 -0.6443 -1.5531
##  [25] -1.5977  1.8051 -0.4816  0.6204  0.6121 -0.1623
##  [31]  0.8119  2.1968  2.0492  1.6324  0.2543  0.4912
##  [37] -0.3241 -1.6621  1.7677  0.0258  1.1285 -2.3804
##  [43] -1.0603  0.9371  0.8545  1.4607 -1.4131  0.5674
##  [49]  0.5832 -1.3068 -0.5404  1.9477  0.0536  0.3517
##  [55] -0.6710  0.2780  0.6912  0.8238  2.1451 -2.3469
##  [61]  0.1496 -1.3425  0.5533  1.5900 -0.5869 -1.8324
##  [67]  0.8881  1.5935  0.5169 -1.2957  0.0546 -0.7846
##  [73] -1.0494  2.3305  1.4027  0.9426  0.8263 -0.8115
##  [79]  0.4762  1.0213  0.6454  1.0431 -0.3044  2.4771
##  [85]  0.9712  1.8671  0.6720 -0.3080  0.5365  0.8249
##  [91] -0.9639 -0.8551  1.8869 -0.3918 -0.9806  0.6873
##  [97] -0.5050  2.1577 -0.5998 -0.6945

La distribución normal es frecuentemente utilizada para describir la diferencia entre valores observados y valores predichos de un modelo ajustado.

Para entender bien el concepto de áreas baja la curva daremos algunos ejemplos que pueden resolverse con simples funciones de R, siguiendo las reglas básicas de probabilidad.

8.0.1 Determine la probabilidad de z (de la curva normal) con valores que están entre -1.73 y 2.60?

pnorm(2.60)-pnorm(-1.73)

## [1] 0.954

R/ el área bajo la curva normal estándar es de 0.95

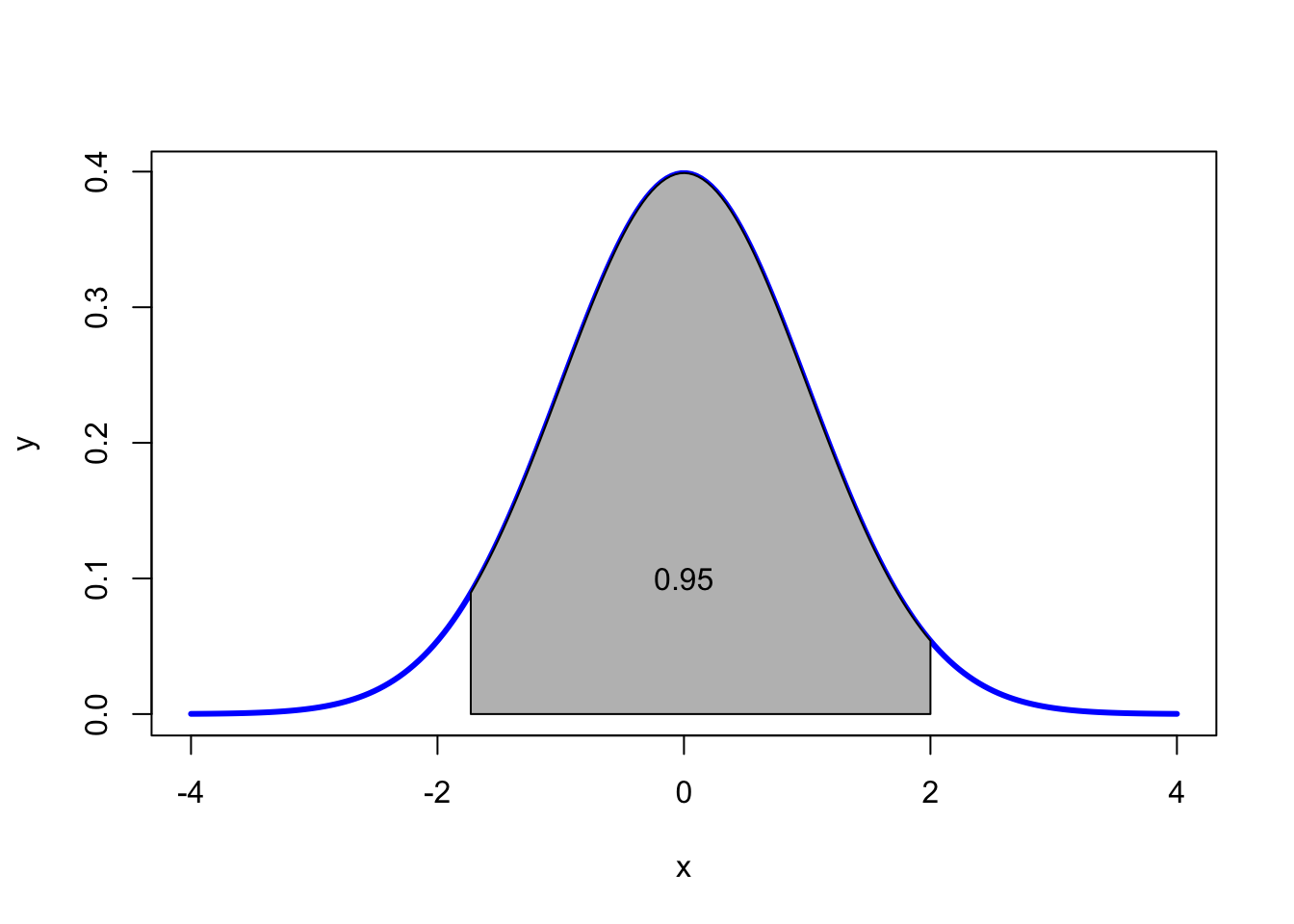
Figura 8.3: Curva normal estándar para una pnorm(2.60)-pnorm(-1.73)

8.0.2 Dada la curva normal estándar, calcular Pr(z mayor igual que 2.65).

1-pnorm(2.65)

## [1] 0.00402

8.0.3 Casos para la curva normal estándar

8.0.3.1 Reglas de la curva normal estándar

Escriba la función, para las siguientes figuras

1) Caso 1

## [1] 0.411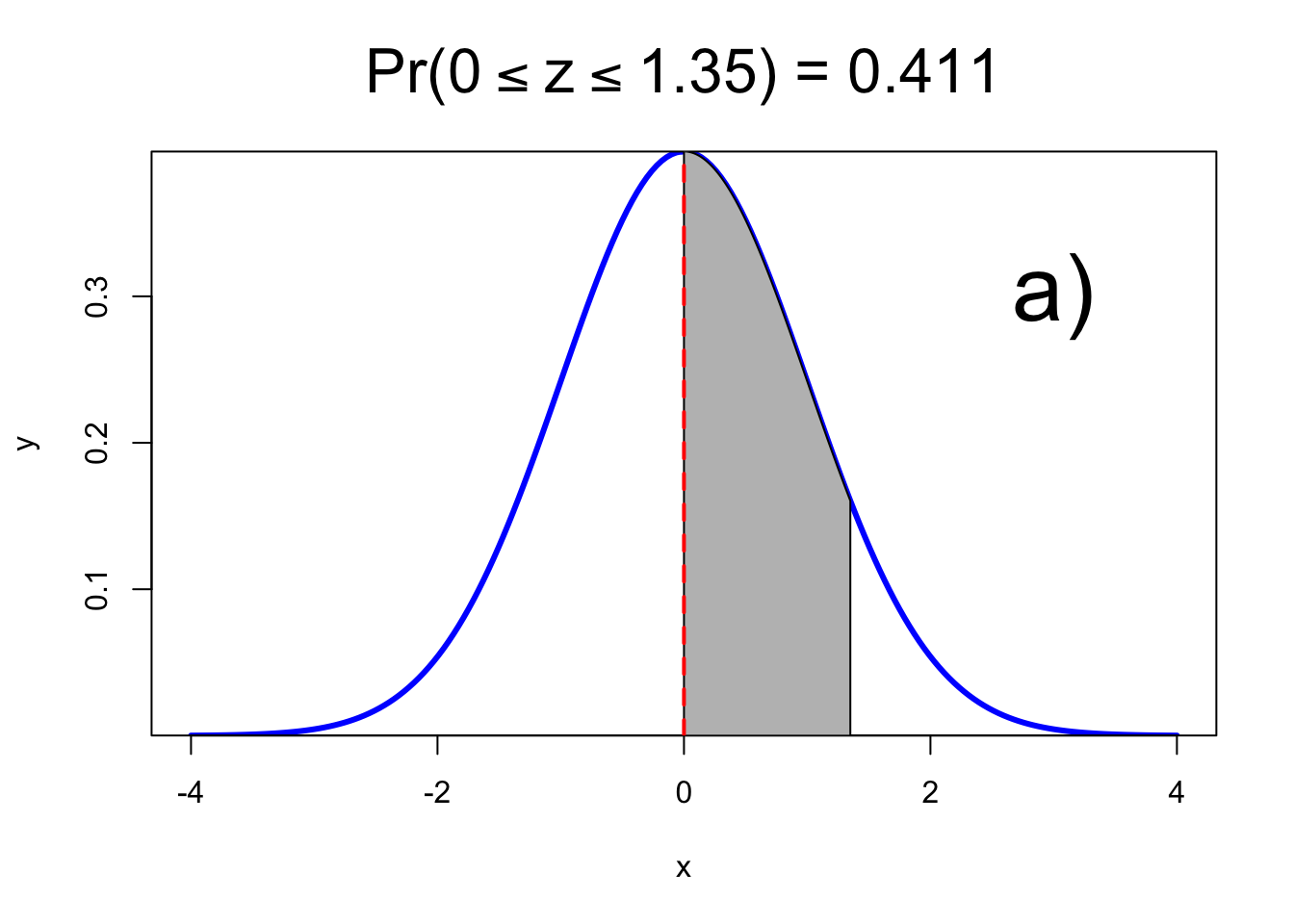

2) Caso 2

## [1] 0.954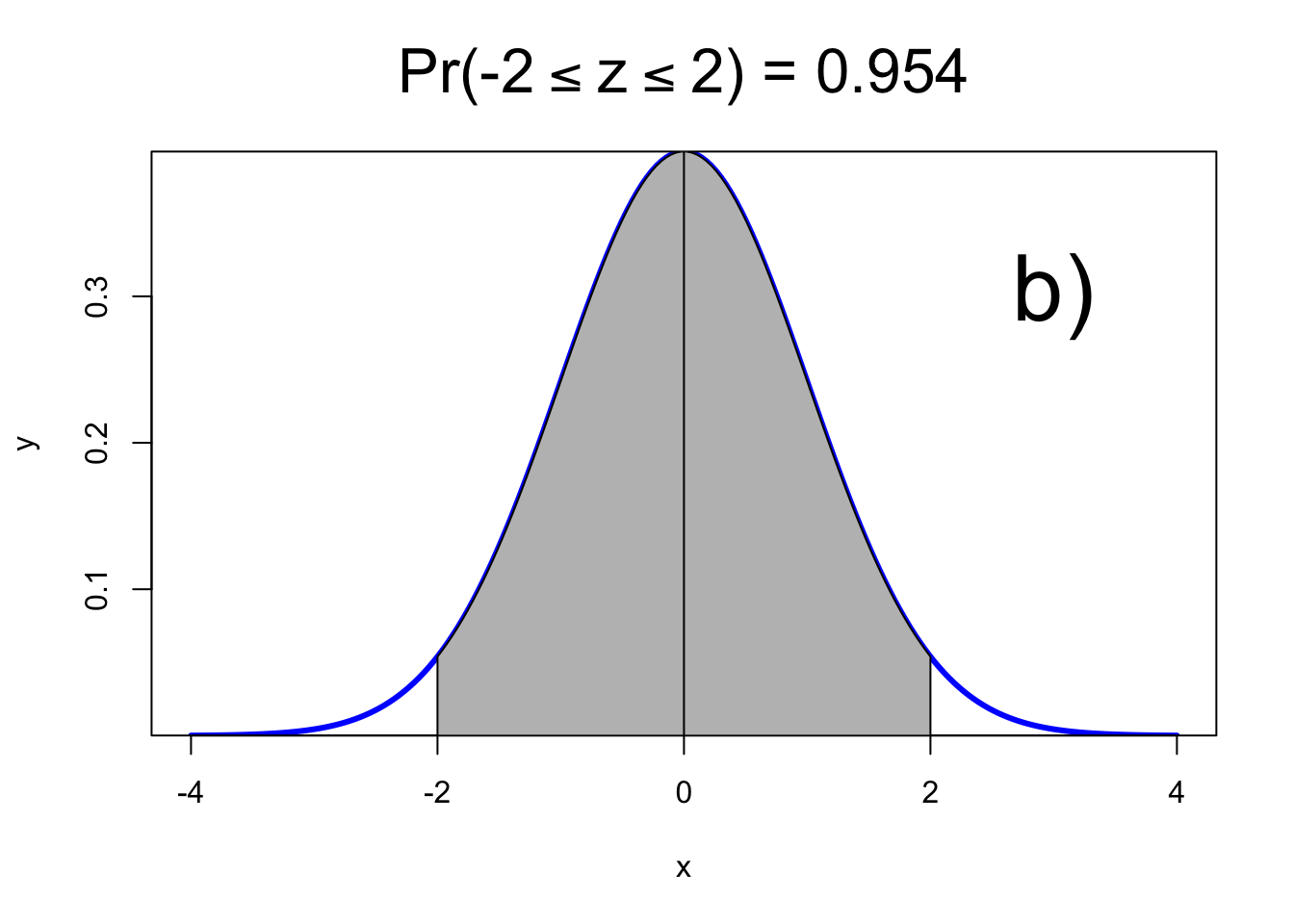

3) Caso 3

## [1] 0.841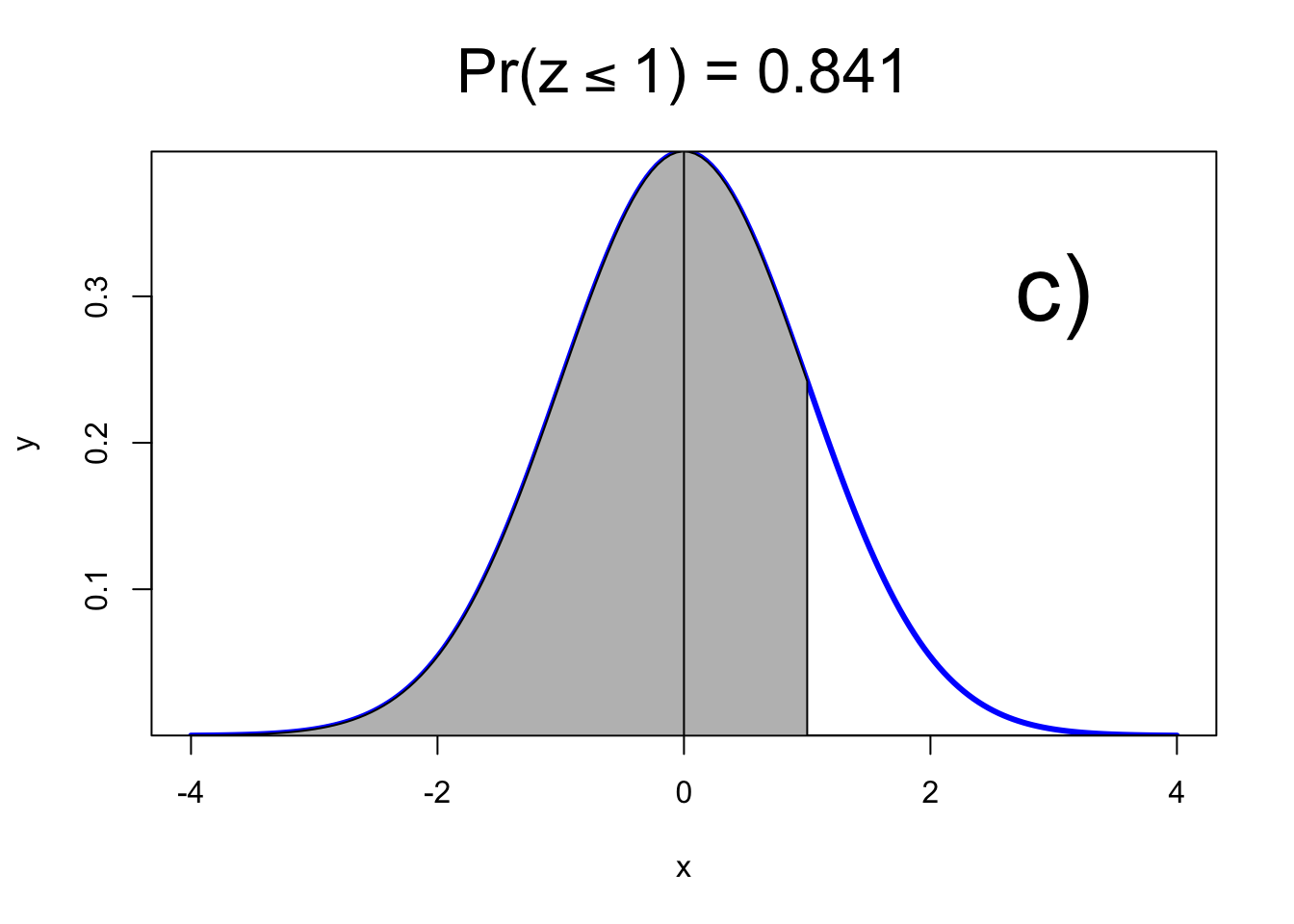

4) Caso 4

## [1] 0.977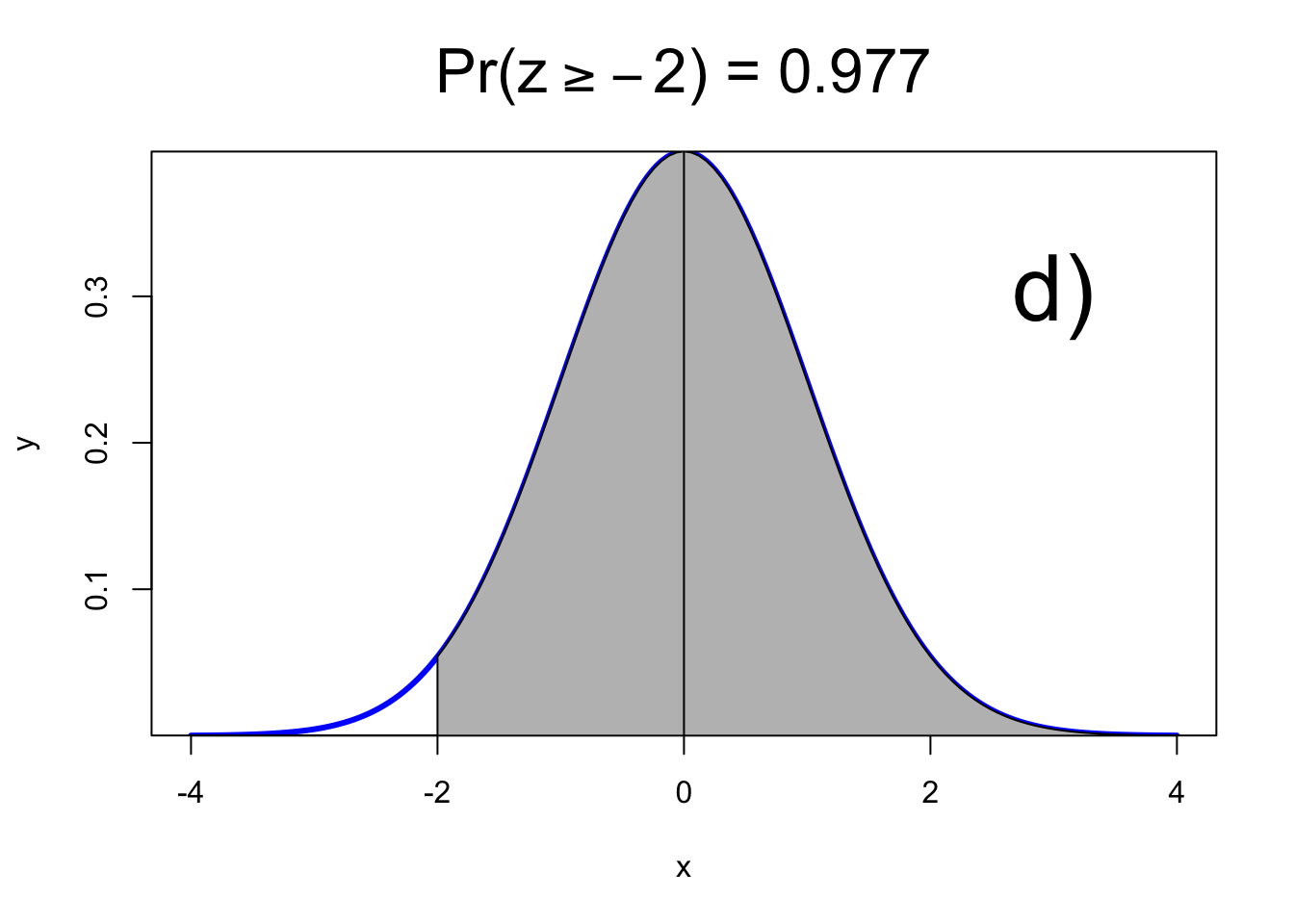

5) Caso 5

## [1] 0.136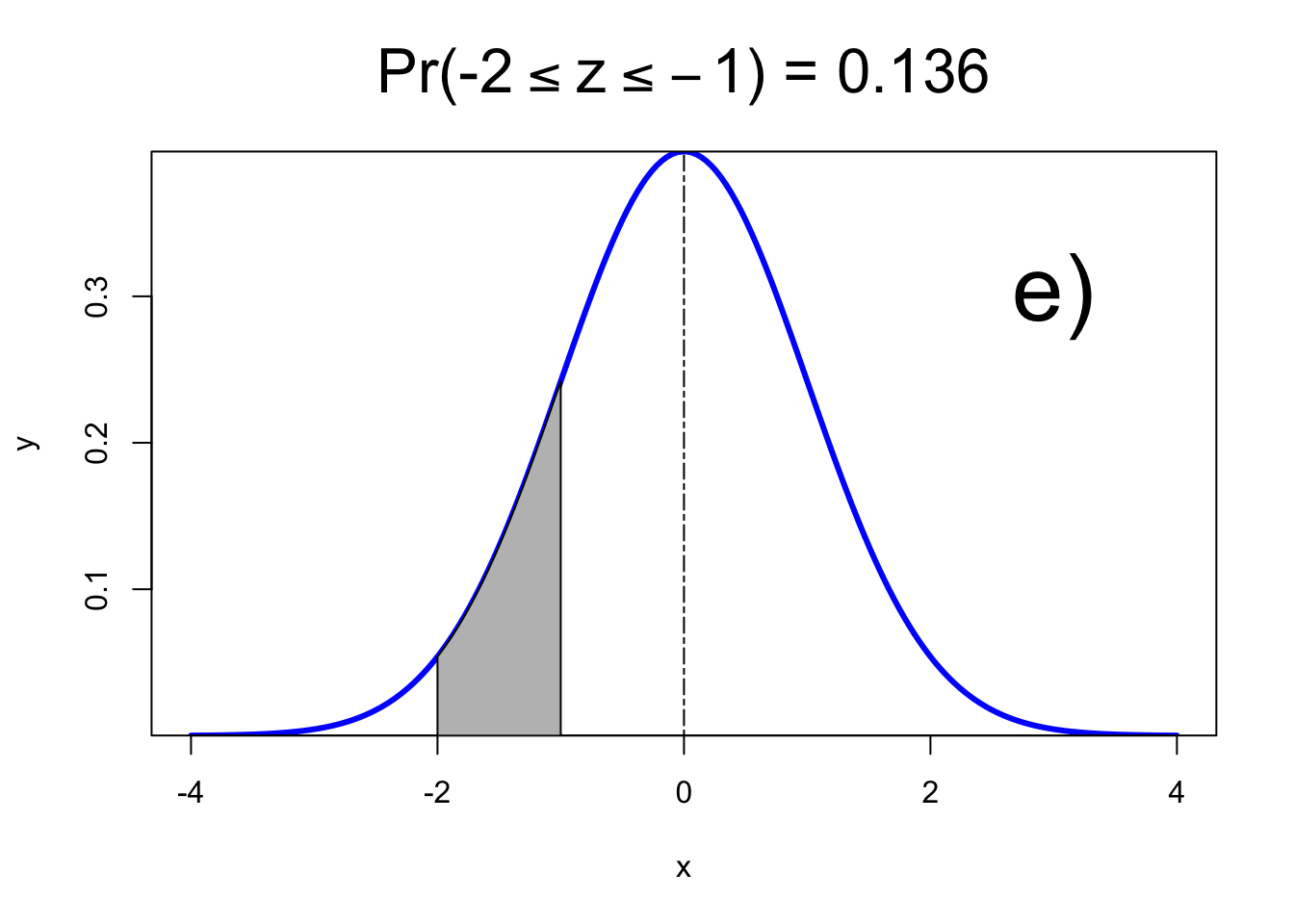

6) Caso 6

## [1] 0.136

8.1 Aplicación de la curva normal estándar.

Los parámetros de estimación de la distribución normal son la media y desviación típica . Cualquier observación de x sobre la línea base de la curva normal se puede estandarizar como el número de unidades de desviaciones típicas.

La forma de responder a cuestiones de probabilidad acerca de variables continuas aleatorias esta dado por:

\[z=\frac{x-\mu }{\sigma}\]

A menudo sucede que desconocemos los valores de la media. y de desviación típica. Es por lo que utilizamos los estadísticos de una muestra dados por el promedio y la desviación estándar (s) y se consideran buenos estimadores de la media y la varianza

\[z=\frac{x- \overline{x}}{s}\]

Estandarizando una observación x su valor z, podemos relacionarlo con las propiedades de las curvas normales.

require(TeachingDemos) # Carga la extensión

## Loading required package: TeachingDemos

8.1.1 Un estudio acerca de la estructura de árboles, determino que la población de la especie de Cecropias en la zona del Caribe tienen una media en DAP cercana a los 63 cm con una desviación estándar de 4.4 cm. Se quisiera determinar otras mediaciones en una zona próxima y suponiendo que los datos pertenecen a una población grande con una distribución aproximadamente normal.

8.1.2 Es posible encontrar arboles con DAP igual a 60 cm que pertenezcan a esa misma población?

Solución.

z.test(x=60,mu=63,sd=4.4, alternative = "two.sided")

## 
##  One Sample z-test
## 
## data:  60
## z = -0.7, n = 1, Std. Dev. = 4, Std. Dev. of the
## sample mean = 4, p-value = 0.5
## alternative hypothesis: true mean is not equal to 63
## 95 percent confidence interval:
##  51.4 68.6
## sample estimates:
## mean of 60 
##         60

pnorm(60,63,4.4)*2

## [1] 0.495

Nota: Entender que la pregunta es en masa y la función dnorm no calcula en masa, calcula la densidad, es por ello por lo que para convertir la respuesta a una función en masa la multiplicamos por dos, de esta manera tendremos la solución. Esto opción solo aplica cuando la pregunta es menor a la media, en este caso la pregunta era a 60 y nuestra media es mayor “63”

Nota 2: Cuando la pregunta en masa, tiene un valor que supera la media se debe aplicar (1-pnorm(x))*2.

8.1.3 Determine si es posible encontrar árboles con DAP igual a 67 cm que pertenezcan a esa misma población?

(1-pnorm(67,63,4.4))*2

## [1] 0.363

Mismo resultado que obtenemos con z.test

z.test(67,63,4.4)

## 
##  One Sample z-test
## 
## data:  67
## z = 0.9, n = 1, Std. Dev. = 4, Std. Dev. of the
## sample mean = 4, p-value = 0.4
## alternative hypothesis: true mean is not equal to 63
## 95 percent confidence interval:
##  58.4 75.6
## sample estimates:
## mean of 67 
##         67

Observe que esta aplicación “TeachingDeamos” nos brinda el resultado de z = -0.6818, y la probabilidad de que el evento ocurra: p-value = 0.4954. Así mismo nos calcula el intervalo de confianza = [51.37 a 68.62].

La función “pnorm” únicamente nos permite calcular la probabilidad. Esta es reducida en cuanto a la información brindada, no permite calcular un nivel de significación diferente al 95% como si lo hace “z.test”, pero es suficiente para responder lo que nos interesa.

Las áreas de rechazo al 95% de confianza en la curva normal estándar están determinadas por 1.96 desviaciones estándar a cada lado.

Curva normal estándar, al 95 % de confianza mostrando sus áreas de aceptación de la curva normal.

Como observa el valor de z (-0.68) cae dentro del área de aceptación de más menos 1.96 desviaciones estándar.

R/ Se puede determinar que arboles con DAP igual a 60 cm pertenecen a esa población con una confiabilidad del 95%.

Con base al área de rechazo de z=-0.68, podríamos concluir, además, si se nos hubiese planteado la hipótesis que:

H0= DAP =60 H1= DAP dif 60.

Si se planteara la pregunta:

8.1.4 Determine la probabilidad de encontrar arboles con DAP mayores a 70 cm, dentro de la población.

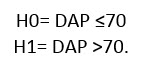
Note que ahora estamos interesados en conocer la probabilidad de un evento dado.

Solución:

z.test(70,63,4.4,alternative="greater")

## 
##  One Sample z-test
## 
## data:  70
## z = 2, n = 1, Std. Dev. = 4, Std. Dev. of the
## sample mean = 4, p-value = 0.06
## alternative hypothesis: true mean is greater than 63
## 95 percent confidence interval:
##  62.8  Inf
## sample estimates:
## mean of 70 
##         70

1-pnorm(70,63,4.4)

## [1] 0.0558

8.1.4.1 Calculando el valor de z

qnorm(0.05581502, lower.tail = FALSE)

## [1] 1.59

Note que la función “qnorm” nos permite calcular el valor de z estandarizado de los datos. Esto únicamente funciona para funciones acumuladas. Siempre debe utilizar lower.tail = FALSE, para que dé el verdadero valor de z, sino el valor podría tener un símbolo diferente.

Compare sus resultados utilizando “TeachingDeamos” y “pnorm”. Deben de coincidir.

Nota: Verifique también el uso de la tabla de normal estándar para contrastar su respuesta.

También podemos hacer uso directo definiendo la hipótesis alternativa en el comando de z.test.

R/ la probabilidad de encontrar arboles con DAP mayores a 70 es de un 5%.

8.1.5 Probabilidad de encontrar árboles mayores a 55 cm.

z.test(55,63,4.4, alternative="g")

## 
##  One Sample z-test
## 
## data:  55
## z = -2, n = 1, Std. Dev. = 4, Std. Dev. of the
## sample mean = 4, p-value = 1
## alternative hypothesis: true mean is greater than 63
## 95 percent confidence interval:
##  47.8  Inf
## sample estimates:
## mean of 55 
##         55

1-pnorm(-1.8182)

## [1] 0.965

R/ la probabilidad de encontrar arboles mayores a 55 cm es de un 96%.

8.1.6 Se realiza un estudio para conocer los ámbitos de acción de especies de perezosos durante un periodo de un mes, se seleccionan de manera aleatoria de la población 35 individuos. Los datos fueron registrados en hectáreas por mes.

ra<-c(8.08,6.33,7.88,10.98,7.81,6.49,9.67,9.17,9.06,9.77,8.89,6.06,7.86,6.86,11.79,4.88,10.42,4.98,6.25,7.04,7.76,5.33,4.98,7,8.74,7.14,6.73,7.79,9.48,8.86,6.29,9.73,9,5.39,7.56)
ra

##  [1]  8.08  6.33  7.88 10.98  7.81  6.49  9.67  9.17
##  [9]  9.06  9.77  8.89  6.06  7.86  6.86 11.79  4.88
## [17] 10.42  4.98  6.25  7.04  7.76  5.33  4.98  7.00
## [25]  8.74  7.14  6.73  7.79  9.48  8.86  6.29  9.73
## [33]  9.00  5.39  7.56

8.1.7 Cual es la probabilidad de encontrar un individuo dentro de la población cuyo ámbito de acción sea igual a 7.5?

mean(ra)

## [1] 7.77

sd(ra)

## [1] 1.77