Cap. 10 Distribución Discreta
Ejercicio1. 1. Diez individuos, cada uno de ellos propenso a la tuberculosis, entran en contacto con un portador de la enfermedad. La probabilidad de que la enfermedad se contagie del portador a un sujeto cualquiera es de 0.1.
1.a Cuántos se espera que contraigan la enfermedad?
Solución:
## [1] 0.387Revisamos el comportamiento para todos los eventos.
## Eventos Prob
## 1 0 3.49e-01
## 2 1 3.87e-01
## 3 2 1.94e-01
## 4 3 5.74e-02
## 5 4 1.12e-02
## 6 5 1.49e-03
## 7 6 1.38e-04
## 8 7 8.75e-06
## 9 8 3.65e-07
## 10 9 9.00e-09
## 11 10 1.00e-1010.1 Ejericio
10.1.1 La probabilidad de que cierto antibiótico presente una reacción negativa al administrarse a un ave rapaz en recuperación es de 0.15. Si se les ha administrado dicho antibiótico a 10 aves, calcular las probabilidades de que haya reacción negativa.
10.1.2 En dos aves.**
## [1] 0.27610.1.3 En ningún ave**
## [1] 0.197Explore que podemos calcular el resultante de todos los eventos, hasta los eventos máximos posibles.
## Eventos Prob
## 1 0 1.97e-01
## 2 1 3.47e-01
## 3 2 2.76e-01
## 4 3 1.30e-01
## 5 4 4.01e-02
## 6 5 8.49e-03
## 7 6 1.25e-03
## 8 7 1.26e-04
## 9 8 8.33e-06
## 10 9 3.27e-07
## 11 10 5.77e-09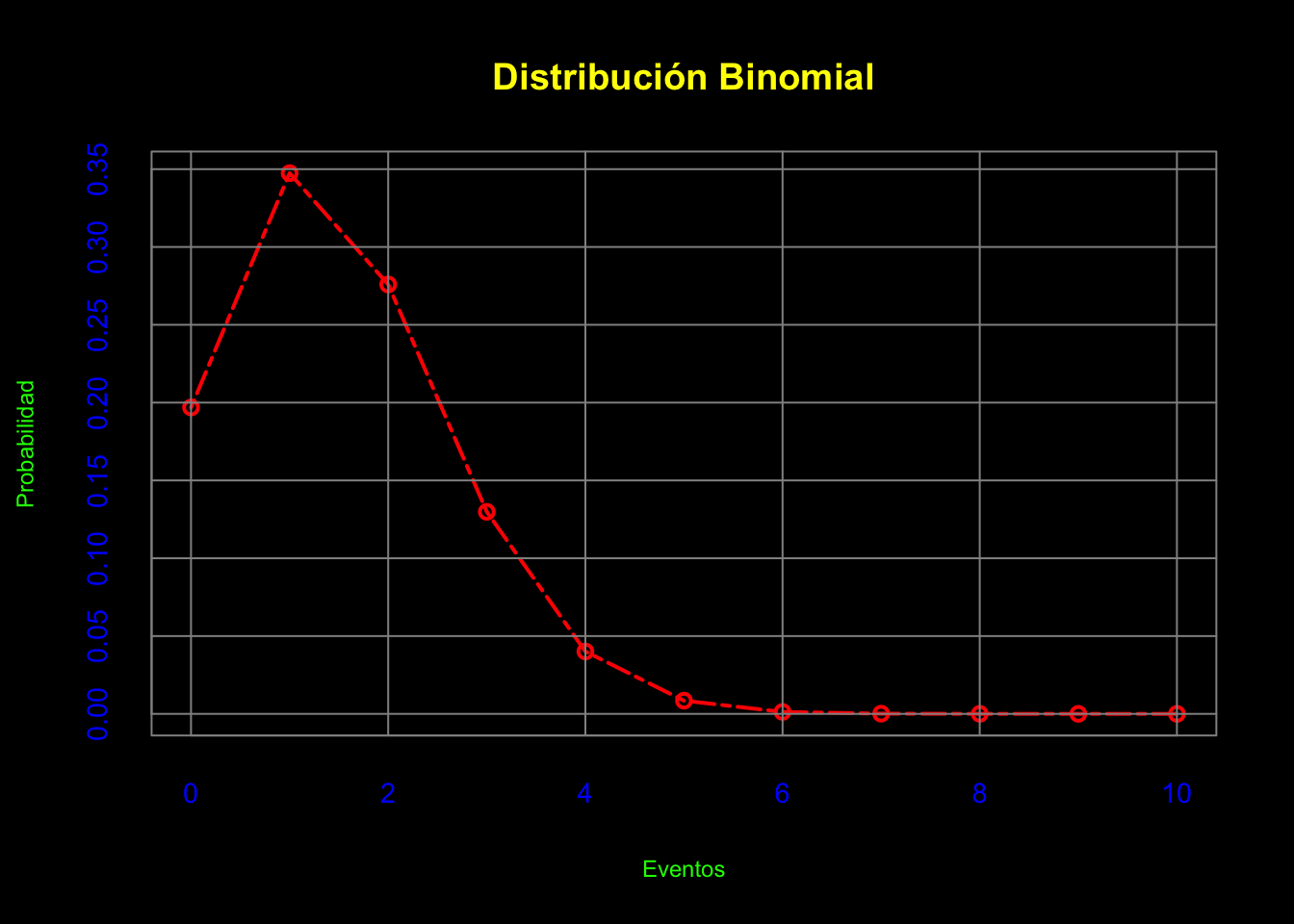
10.2 Ejercicio
10.2.1 En una gasolinera la llegada de veh?culos sigue la Distribución de Poisson de parámetro 1.6. Calcúlese la probabilidad de que?**
10.2.2 El no de vehículos que lleguen sea superior a tres?**
## [1] 0.078810.2.3 Está comprendido entre dos y cinco.**
## [1] 0.46910.2.4 Llegue algún vehículo (P>=1)?**
## [1] 0.79810.2.5 Plot de la distribución cuyos parámetros son de Lambda=1.6, cuya x sea hasta 10 eventos posibles, de una funciín acumulada, de “mas allá de”.**
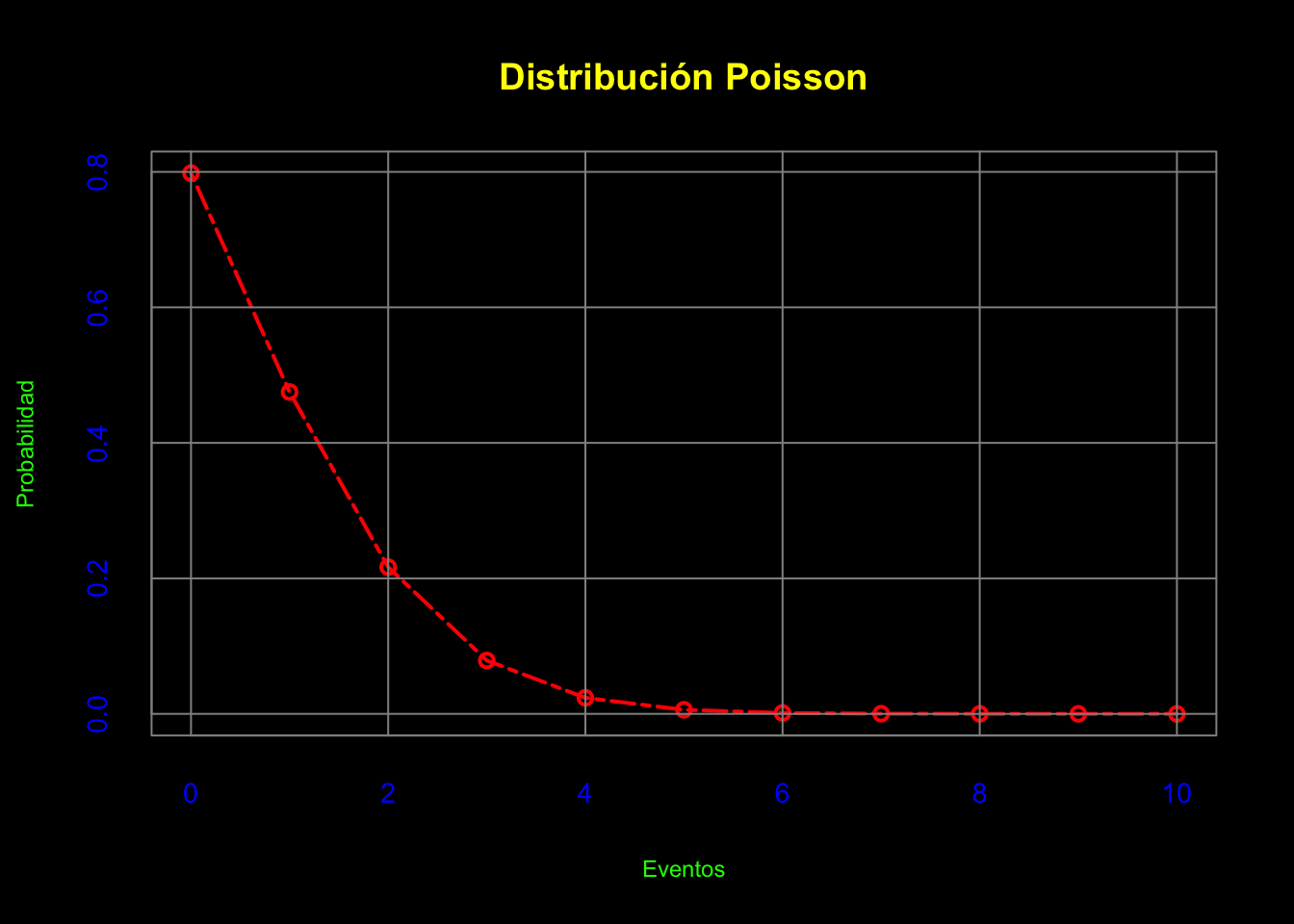
10.2.6 Revisamos el comportamiento para todos los eventos, en un cuadro de resultados (data.frame).**
## Eventos Prob
## 1 0 7.98e-01
## 2 1 4.75e-01
## 3 2 2.17e-01
## 4 3 7.88e-02
## 5 4 2.37e-02
## 6 5 6.04e-03
## 7 6 1.34e-03
## 8 7 2.60e-04
## 9 8 4.54e-05
## 10 9 7.14e-06
## 11 10 1.02e-06Ejercicio 4
10.2.7 Buscar la máxima verosimilitud de una Distribución binomial cuyos parámetros son N=30, P=0.68, de una función en masa.**
## [1] 0.153Ejercicio 5
10.2.8 Plot de la distribución cuyos parámetros son de N=30, P=0.15, de una función en “masa”.**

Ejercicio 6
10.2.9 Una empresa electrónica observa que el número de componentes que fallan antes de cumplir 100 horas de funcionamiento es una variable aleatoria de Poisson. Si el número promedio de estos fallos es ocho.**
10.2.10 Cuál es la probabilidad de que falle un componente en 25 horas?**
## [1] 0.27110.3 Ejericio
10.3.1 Supongamos que el número de imperfecciones en un alambre delgado de cobre sigue una Distribución Poisson con una media de 2.3 imperfecciones por milímetro.**
10.3.2 Determine la probabilidad de 2 imperfecciones en un mil?metro de alambre.**
## [1] 0.26510.3.3 Visualizar todos los posibles eventos (utilice 0:25) de la función anterior.**
## Eventos Prob
## 1 0 1.00e-01
## 2 1 2.31e-01
## 3 2 2.65e-01
## 4 3 2.03e-01
## 5 4 1.17e-01
## 6 5 5.38e-02
## 7 6 2.06e-02
## 8 7 6.77e-03
## 9 8 1.95e-03
## 10 9 4.98e-04
## 11 10 1.14e-04
## 12 11 2.39e-05
## 13 12 4.59e-06
## 14 13 8.12e-07
## 15 14 1.33e-07
## 16 15 2.04e-08
## 17 16 2.94e-09
## 18 17 3.98e-10
## 19 18 5.08e-11
## 20 19 6.15e-12
## 21 20 7.07e-13
## 22 21 7.75e-14
## 23 22 8.10e-15
## 24 23 8.10e-16
## 25 24 7.76e-17
## 26 25 7.14e-18
10.4 Ejercicio
Determine la probabilidad de 10 imperfecciones en 5 milímetros de alambre.
## [1] 0.113Se debe calcular el lambda para 5 mm. Por eso es que se utiliza regla de tres.
10.5 Ejericio
10.5.1 En una empresa el término medio de accidentes es de 3 por mes. Calcular la probabilidad de:**
8a. Que no ocurra ning?n accidente en un mes.
## [1] 0.049810.5.2 Que ocurran 30 accidentes en un año.**
## [1] 0.042710.5.3 Visualizar todos los eventos posibles, para encontrar la máxima verosilitud de la distribución Poisson de los datos brindados en el problema anterior (utilice de 0:36 para este ejercicio).**
## [1] 0.066310.5.4 Visualización gráfica, utilice hasta 60 eventos para determinar la máxima verosimilitud.**

## [1] 0.0663