Cap. 6 Probabilidad Discreta

Se les denomina discretas, debido a que sus eventos no asumen valores intermedios entre dos números enteros, entre las distribuciones mas comunes tenemos: . Binomial: binom . Poisson: pois . Hipergeométrica: hyper . Binomial negativa: nbinom . Geométrica: geom.

Las funciones de probabilidad pueden ser formuladas de la siguiente manera:

Masa: Necesario anteponerle el prefijo “d”, por ejemplo:

. dbinom(x) #función de la distribución binomial.

. Acumuladas: Necesario anteponerle el prefijo “p”, por ejemplo:

. pbinom(x) #función de la distribución binomial.

y “q” para la función cuantil (inversa de la función de distribución).

. qbinom(p, size) #siendo “p” la probabilidad y “size” el tamaño de la muestra.

Donde para cualquier función: P= es la probabilidad que de ocurra el evento q= 1-P= probabilidad de que no ocurra el evento

Podemos identificar estas funciones cuando la pregunta incluye las siguientes palabras claves.

6.1 USE LA FUNCION MASA

Cuando el problema contenga palabras claves como: Ejem.

6.2 USE LA FUNCION ACUMULADA

Cuando usted quiere responder a lo siguiente:

Nota: Este tipo de reglas (función en masa y acumulada) para la distribución continua son similares, excepto que siempre se utiliza el valor que se esta indagando (nunca se utilizan el numero mas próximo). Ver ejemplos mas adelante.

6.3 Probabilidad Binomial

Es una de las probabilidades mas útiles en los diferentes campos que se pueden aplicar, tanto en biología, medicina, economía, inspección de calidad, opiniones y otras. Se reconoce porque se clasifican los eventos como ocurrencia (éxito) y no ocurrencia de un suceso (fracasos). Las dos suposiciones de esta distribución son: a) La probabilidad de éxito permanece constante b) Los n ensayos son independientes entre si Los parámetros de la distribución binomial están dados por n y p.

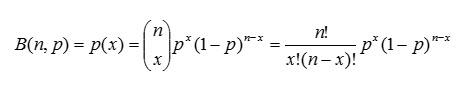
Donde * n son los ensayos * p la probabilidad de éxito.

El modelo binomial tiene tres propiedades que lo definen:

Los ensayos de Bernoulli se llevan a cabo n veces,

Los ensayos son independientes,

La probabilidad de éxito p no cambia entre los ensayos.

Se le conoce también como distribución de la probabilidad puntual o de Bernoulli, debido al suizo Jacques Bernoulli, quien por primera vez desarrollo el concepto de ensayos independientes.

6.4 Ejemplos

Se conoce que el musgo es un inhibidor de la floración en plantaciones de cacao. Se realiza un experimento con un tipo de fertilizante orgánico para eliminar el musgo en una plantación de cacao orgánico. Se encontró una efectividad del fertilizante en los primeros experimentos del 75%. Encontrar la probabilidad de que se aplique el mismo fertilizante en otras fincas de cacao orgánico en 10 parcelas del mismo tamaño y bajo las mismas condiciones.

6.4.1 Determine cual es la probabilidad de que exactamente 3 parcelas no pierdan su cosecha?**

Solución. n = 10; x = 3 parcelas no pierdan su cosecha; p = 0,75; q = 0,25. Siendo p el éxito y q el fracaso.

Pr(X=3)= dbinom(3,10,0.75)

dbinom(3,10,0.75)
## [1] 0.00309

R/ la probabilidad de que exactamente 3 parcelas no pierdan su cosecha es de un 0.3% (multiplica su resultado por 100).

6.4.2 Cual es la probabilidad de que exactamente 3 parcelas pierdan su cosecha?**

Solución. n = 10; x = 3 parcelas pierdan su cosecha; p = 0,25; q = 0,75, en este caso estamos interesados en que el éxito sea la perdida por tal si la efectividad es del 75%, entonces la perdida es 25%, por lo que p = 0,25 y q = 0,75 asumen esos valores de manera invertida.

dbinom(3,10,0.25)
## [1] 0.25

6.4.3 Al menos 3 parcelas tengan perdida de cosecha.**

Solución. n = 10; x = 3 parcelas pierdan su cosecha; p = 0,25; q = 0,75. Por lo menos es una función acumulada y utiliza la regla de complementación= 1-p.

1-pbinom(2,10,0.25)
## [1] 0.474

R/ la probabilidad de que Al menos 3 parcelas pierdan su cosecha es de un 47.44%

6.4.4 Un reciente estudio indica que los estudiantes de universidades de primer ingreso a carrera utilizan aproximadamente 35.4% el recurso de libros impresos para obtener su información de trabajos o tareas. Sea x una variable aleatoria binomial, y con base a una muestra aleatoria de n=23, utilizada como fuente para obtención del dato.

6.4.5 Encuentre la probabilidad que de x sea igual a 5. Dicho de otra forma, de que 5 estudiantes utilicen libros impresos.**

Solución. n = 23; x = 5; p = 0.354; q = 0.646

dbinom(5, size = 23, prob = 0.354)
## [1] 0.0718

6.4.6 Encuentre la probabilidad de que al menos x sea de 7.** Solución. n = 23; x = 7; p = 0.354; q = 0.646

1-pbinom(6, size = 23, prob = 0.354)
## [1] 0.759

6.4.7 Calcular la probabilidad de que una variable aleatoria binomial de parámetros n=15, p=0.4 tome el valor 7.

Solución.

dbinom(7,size=15,prob=0.4)
## [1] 0.177

6.4.8 Encontrar que cuantil de una variable aleatoria binomial de parámetros n=15,

p=0.4 tome el valor 5:

Solución. n = 15; q = 0.25; p = 0.4; q = 0.6

qbinom(.25,15,0.4)
## [1] 5

Esto nos brinda los menores valores que puede asumir el cuantil 25.

Para su mejor interpretación generaremos de forma aleatoria 100 valores con distribución binomial de parámetros n=15, p=0.4 tome el valor 7.

set.seed(12345)
birandom<-rbinom(100,15,0.4); sort(birandom)
##   [1]  1  2  2  2  3  3  3  3  3  3  3  3  4  4  4  4
##  [17]  4  4  4  4  4  4  5  5  5  5  5  5  5  5  5  5
##  [33]  5  5  5  5  5  5  5  5  5  6  6  6  6  6  6  6
##  [49]  6  6  6  6  6  6  6  6  6  7  7  7  7  7  7  7
##  [65]  7  7  7  7  7  7  7  7  7  7  7  7  7  7  8  8
##  [81]  8  8  8  8  8  8  8  8  8  9  9  9  9  9  9  9
##  [97]  9 10 10 10

Observe que de los 100 valores generados de forma aleatoria con los parámetros establecidos, estamos buscando si es posible encontrar el valor de 7. Efectivamente si es posible dentro de los valores, por lo que utilizamos cuartiles para identificar la posición de ese valor (7). Algunas veces habrá que probar (prueba y error), que valor se aproxima al valor que estamos buscando.

6.4.9 Encontrar el percentil 73 de una variable aleatoria binomial de parámetros n=15,

p=0.4:

Solución. n = 15; q = 0.73; p = 0.4; q = 0.6

qbinom(.73,15,0.4)
## [1] 7

6.4.10 Encontrar el percentil (x) de una variable aleatoria binomial de parametros n=15, p=0.4, que tome el valor 4:**

Solución.

n = 15; q = x; p = 0.4; q = 0.6

qbinom(.4,15,0.4)
## [1] 5

Observe que si utilizamos el percentil 4 la solución NO ES LA CORRECTA, porque toma el valor de 5.

cambiamos los valores a 0.1

qbinom(0.1,15,0.4)
## [1] 4

Nos brinda la respuesta que estamos buscando.

6.5 Forma gráfica de la distribución binomial

Observemos el comportamiento en forma gráfica del caso de las parcelas experimentales que hemos venido desarrollando

6.5.1 n = 10; x = 0:10 parcelas no pierdan su cosecha; p = 0.75; q = 0.25.**

y<-dbinom(0:10,10,0.75)
cbind(x=0:10,datos=y) #crear una cuadro de resultados
##        x    datos
##  [1,]  0 9.54e-07
##  [2,]  1 2.86e-05
##  [3,]  2 3.86e-04
##  [4,]  3 3.09e-03
##  [5,]  4 1.62e-02
##  [6,]  5 5.84e-02
##  [7,]  6 1.46e-01
##  [8,]  7 2.50e-01
##  [9,]  8 2.82e-01
## [10,]  9 1.88e-01
## [11,] 10 5.63e-02
plot(y, type="o", col="red")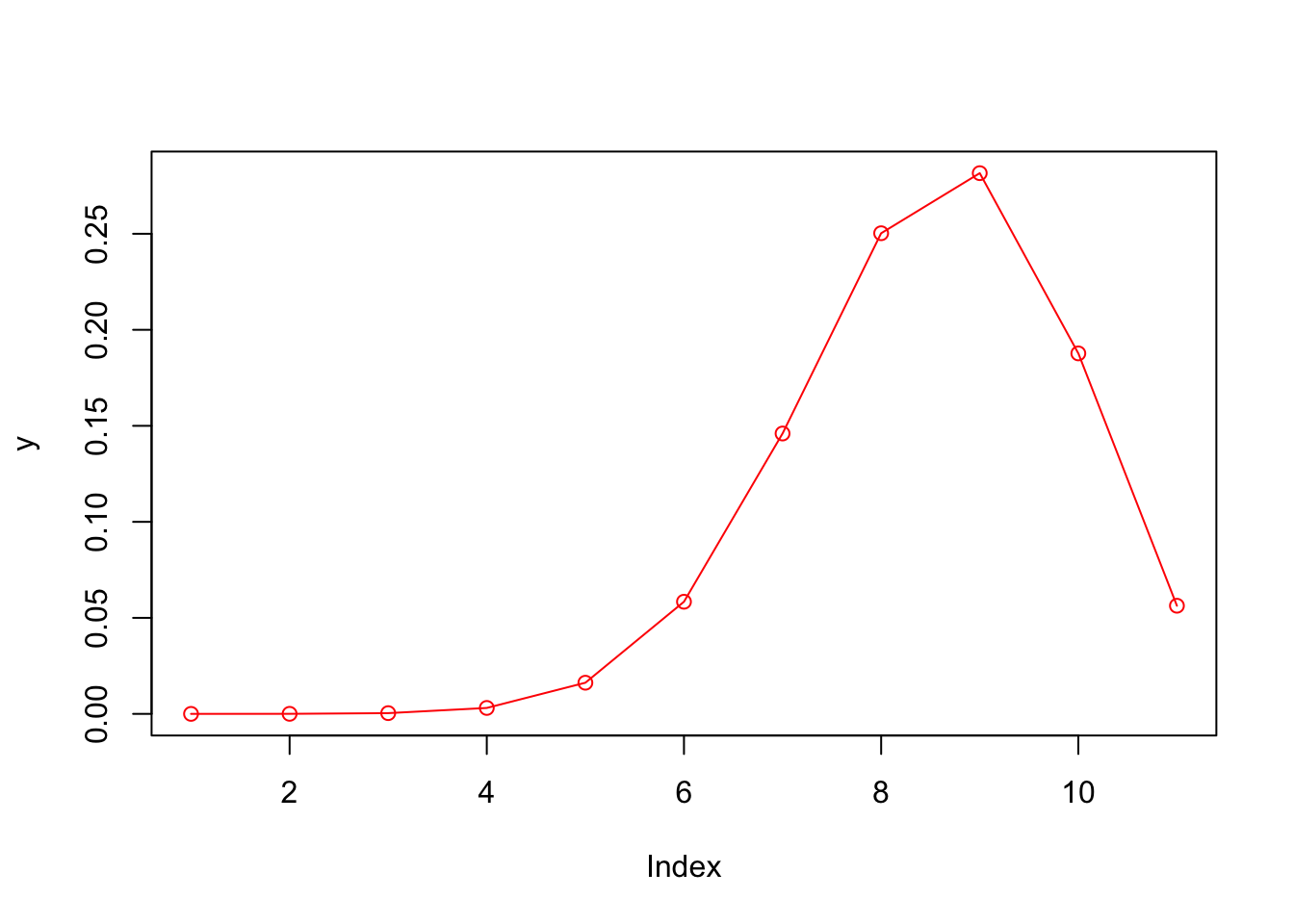
Plot de la distribucion binomial, para n = 0:10; x = 3, p = 0.75.

Figura 6.1: Plot de la distribucion binomial, para n = 0:10; x = 3, p = 0.75.

6.5.2 n = 10; x = 0:10 parcelas pierdan su cosecha; p = 0,25; q = 0,75.**

x<-0:10
z<-dbinom(0:10,10,0.25)
cbind(eventos=0:10,datos=z)
##       eventos    datos
##  [1,]       0 5.63e-02
##  [2,]       1 1.88e-01
##  [3,]       2 2.82e-01
##  [4,]       3 2.50e-01
##  [5,]       4 1.46e-01
##  [6,]       5 5.84e-02
##  [7,]       6 1.62e-02
##  [8,]       7 3.09e-03
##  [9,]       8 3.86e-04
## [10,]       9 2.86e-05
## [11,]      10 9.54e-07
#o puede utilizar tambien el comando de data.frame
data.frame(x,z)  
##     x        z
## 1   0 5.63e-02
## 2   1 1.88e-01
## 3   2 2.82e-01
## 4   3 2.50e-01
## 5   4 1.46e-01
## 6   5 5.84e-02
## 7   6 1.62e-02
## 8   7 3.09e-03
## 9   8 3.86e-04
## 10  9 2.86e-05
## 11 10 9.54e-07
plot(z, type="o", col="orange")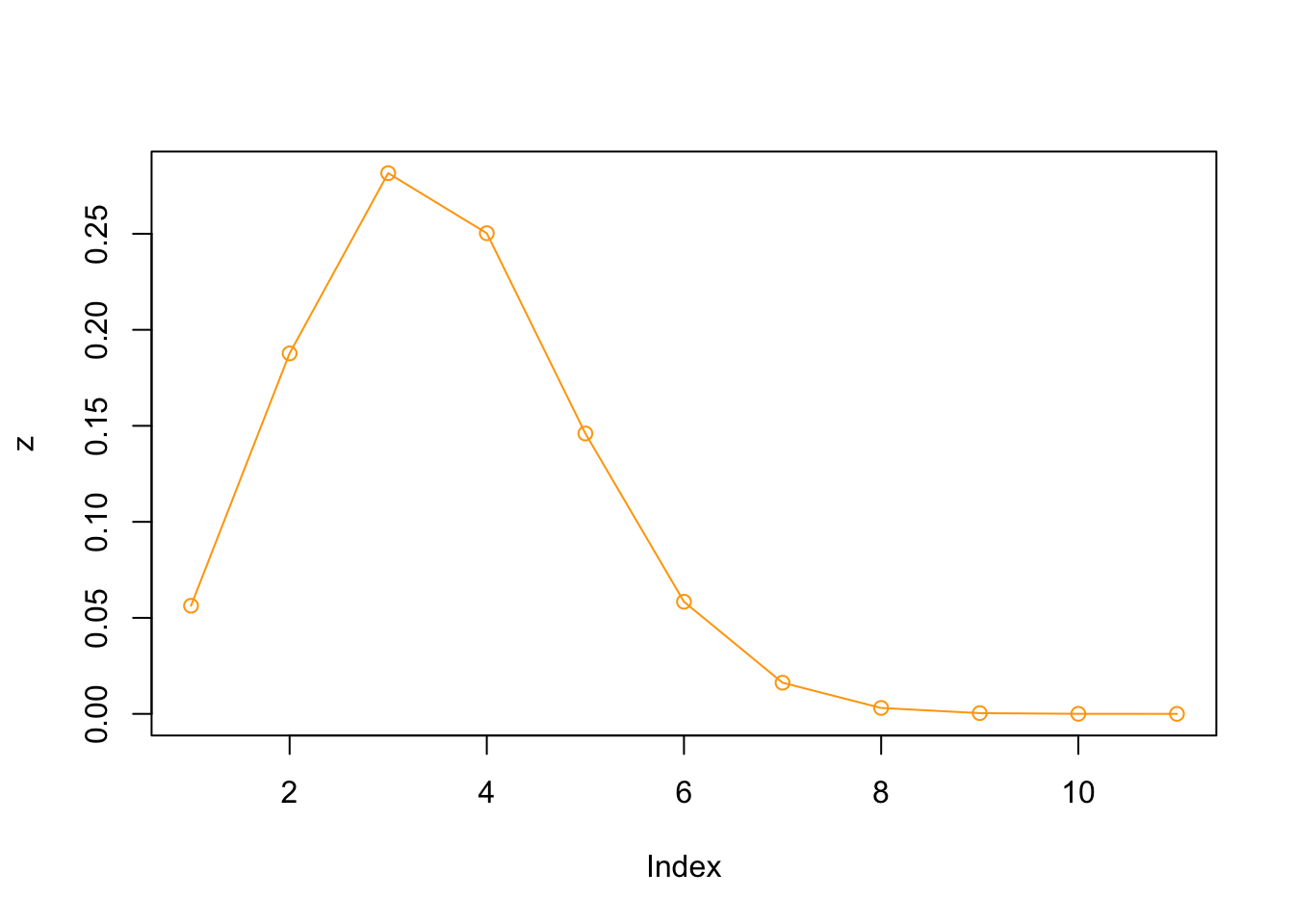
Plot de la distribucion binomial, para n = 0:10; x = 3, p = 0.25.

Figura 6.2: Plot de la distribucion binomial, para n = 0:10; x = 3, p = 0.25.

Nota: Ver que el plot no inicia desde “cero”, por lo que el gráfico no es el adecuado. Mas adelante explicaremos que debemos hacer.

6.5.3 Graficar resultados con funciones que involucren la regla de complementación.

6.5.4 Se conoce que la probabilidad que ocurra el evento es de 0.35. Describa como es la probabilidad resultante de por lo menos en 0 a 10 intentos de 10 ensayos tratados.**

Solución. n = 0:10; x = 0:10 ensayos; p = 0.35; q = 0.65.

1-pbinom(0:10,10,0.35)->co
cbind(eventos=0:10,datos=co)
##       eventos    datos
##  [1,]       0 9.87e-01
##  [2,]       1 9.14e-01
##  [3,]       2 7.38e-01
##  [4,]       3 4.86e-01
##  [5,]       4 2.49e-01
##  [6,]       5 9.49e-02
##  [7,]       6 2.60e-02
##  [8,]       7 4.82e-03
##  [9,]       8 5.40e-04
## [10,]       9 2.76e-05
## [11,]      10 0.00e+00

Nota: observe bien sus resultados para que se familiarice que las probabilidades, inician a partir de cero.
[1,] 0 =9.865373e-01., [2,] 1 9.140456e-01… etc.

Debido a que uno puede uno puede también escribir sus resultados de la siguiente manera.

cbind(1-pbinom(0:10,10,0.35))
##           [,1]
##  [1,] 9.87e-01
##  [2,] 9.14e-01
##  [3,] 7.38e-01
##  [4,] 4.86e-01
##  [5,] 2.49e-01
##  [6,] 9.49e-02
##  [7,] 2.60e-02
##  [8,] 4.82e-03
##  [9,] 5.40e-04
## [10,] 2.76e-05
## [11,] 0.00e+00

9.865373e-01 corresponde a cero eventos, 9.140456e-01 a un evento y así sucesivamente, hasta k eventos posibles

Para corregir ese efecto visual en R, que puede confundir al lector lo que recomiendo es generar un vector del mismo tamaño al estamos indagando, en nuestro caso es de 0 a 10.

x<-0:10 
1-pbinom(0:10,10,0.35)-> co
data.frame("Probabilidad"=co,row.names=x)
##    Probabilidad
## 0      9.87e-01
## 1      9.14e-01
## 2      7.38e-01
## 3      4.86e-01
## 4      2.49e-01
## 5      9.49e-02
## 6      2.60e-02
## 7      4.82e-03
## 8      5.40e-04
## 9      2.76e-05
## 10     0.00e+00

Ahora si es posible determinar el valor exacto de cada evento, debido a que hemos generado los valores que corresponden a cada probabilidad

Observe la diferencia si hubiera escrito en código, separado por “coma” en vez del igual.

data.frame("Probabilidad",co,row.names=x)
##    X.Probabilidad.       co
## 0     Probabilidad 9.87e-01
## 1     Probabilidad 9.14e-01
## 2     Probabilidad 7.38e-01
## 3     Probabilidad 4.86e-01
## 4     Probabilidad 2.49e-01
## 5     Probabilidad 9.49e-02
## 6     Probabilidad 2.60e-02
## 7     Probabilidad 4.82e-03
## 8     Probabilidad 5.40e-04
## 9     Probabilidad 2.76e-05
## 10    Probabilidad 0.00e+00
plot(0:10,1-pbinom(0:10,10,0.35),type='h',xlab="0:10",ylab="Prob", sub="p=0.35")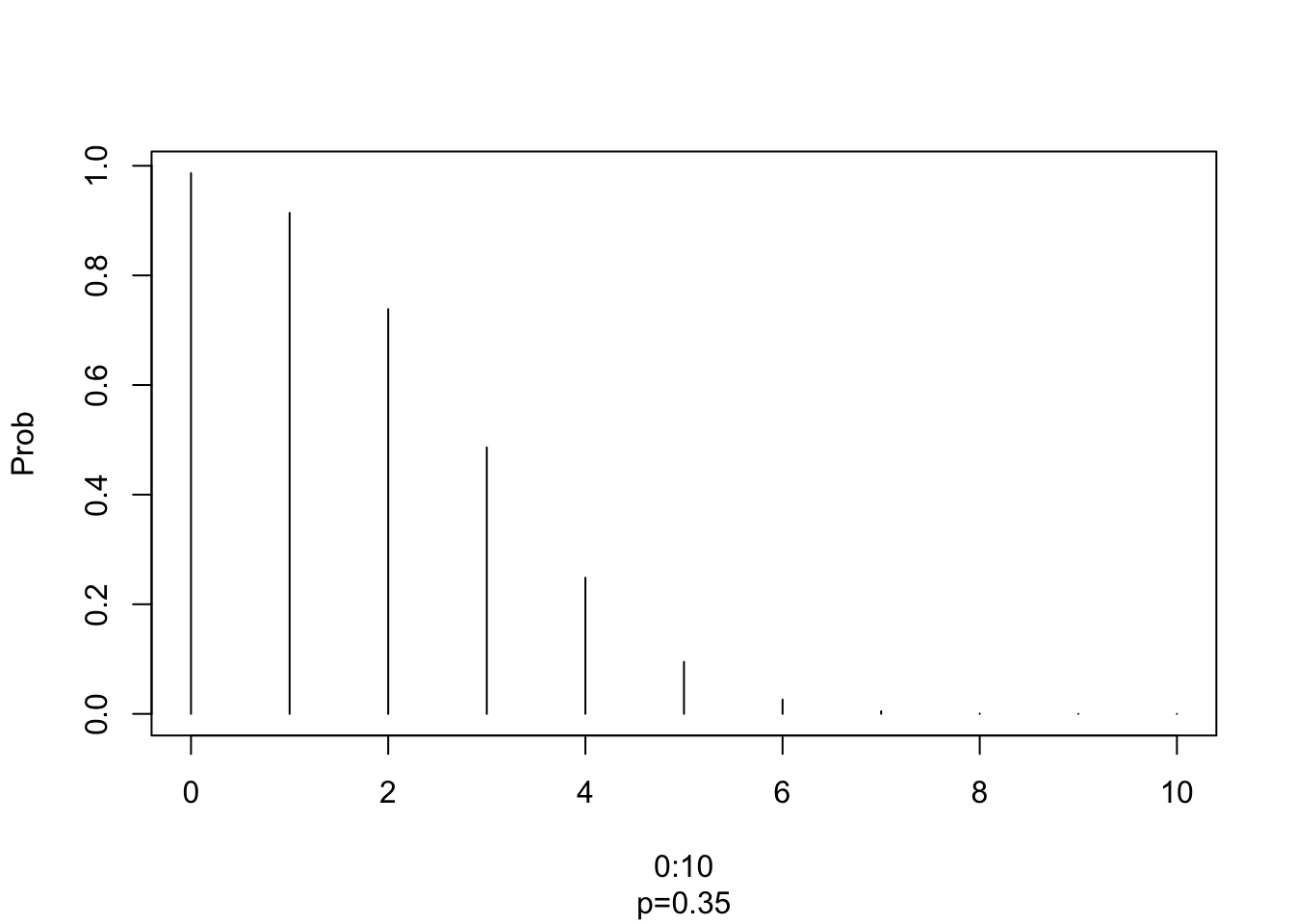
Plot de la distribucion binomial, para n = 0:10; x = 10, p = 0.35.

Figura 6.3: Plot de la distribucion binomial, para n = 0:10; x = 10, p = 0.35.

6.5.5 Se conoce que la probabilidad que ocurra el evento es de 0.65. Describa como es la probabilidad resultante de por lo menos en 0 a 10 intentos de 10 ensayos tratados.***

Solución. n = 0:10; x = 10 ensayos; p = 0.65; q = 0.35.

plot(0:10,1-pbinom(0:10,10,0.65),type='o',xlab="0:10",ylab="Prob", sub="p=0.65")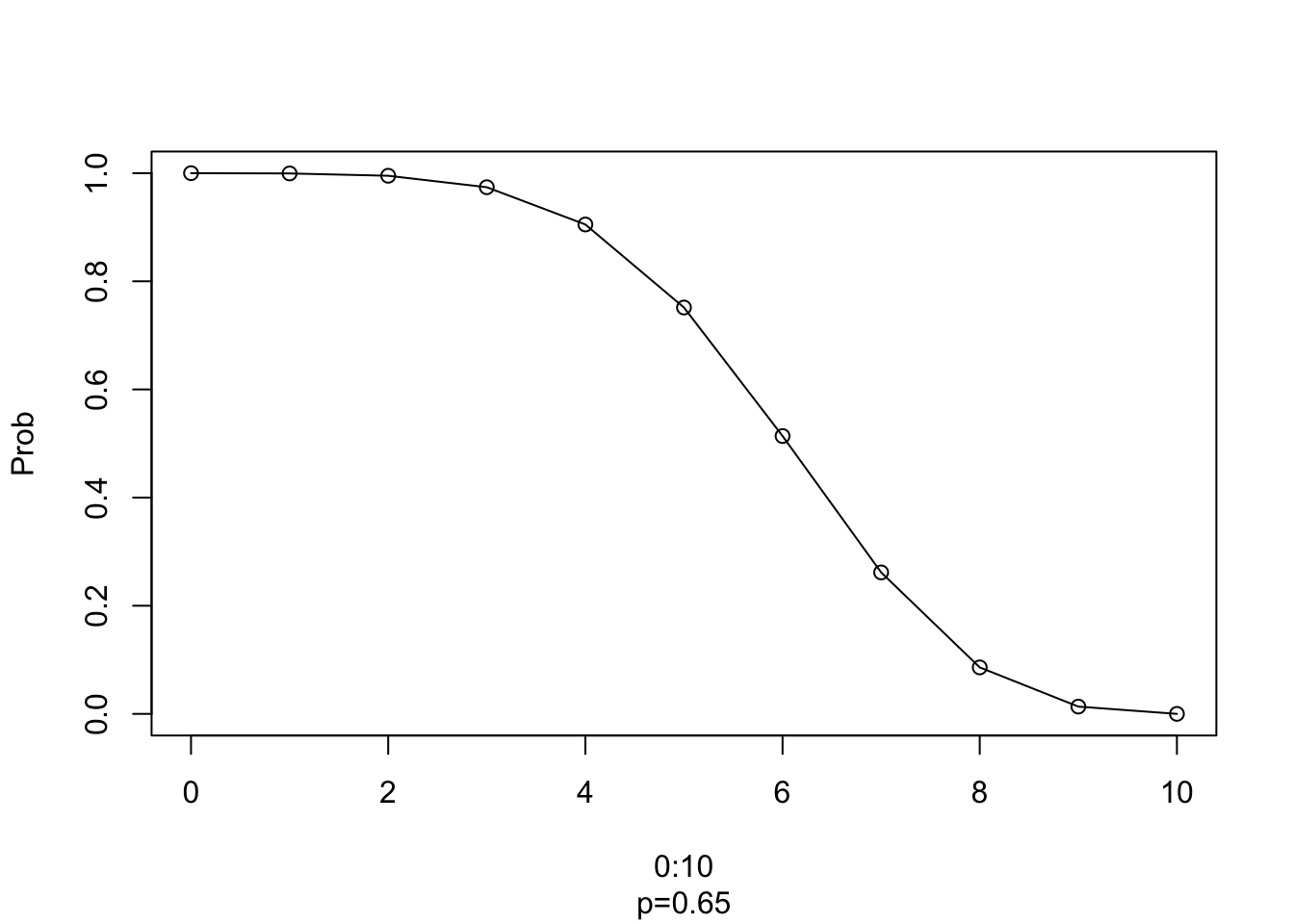
Plot de la distribucion binomial, para n = 0:10; x = 10, p = 0.65.

Figura 6.4: Plot de la distribucion binomial, para n = 0:10; x = 10, p = 0.65.

6.5.6 Obtenga un cuadro resumen utilizando la funcion cbind(., ) de sus resultados.**

6.5.7 Determine cual es la probabilidad de que exactamente 6 eventos, ocurran de los 10 ensayos tratados.**

Graficar resultados que involucren la función en masa.

6.5.8 Se conoce que la probabilidad que ocurra el evento es de 0.35. Describa como es la probabilidad resultante de 0 a 10 intentos de 10 ensayos tratados.**

Solución.

n = 0:10; x = 10 ensayos; p = 0.35; q = 0.65.

plot(0:10, dbinom(0:10,10,0.35),type='o',xlab="0:10",ylab="Prob", sub="p=0.35")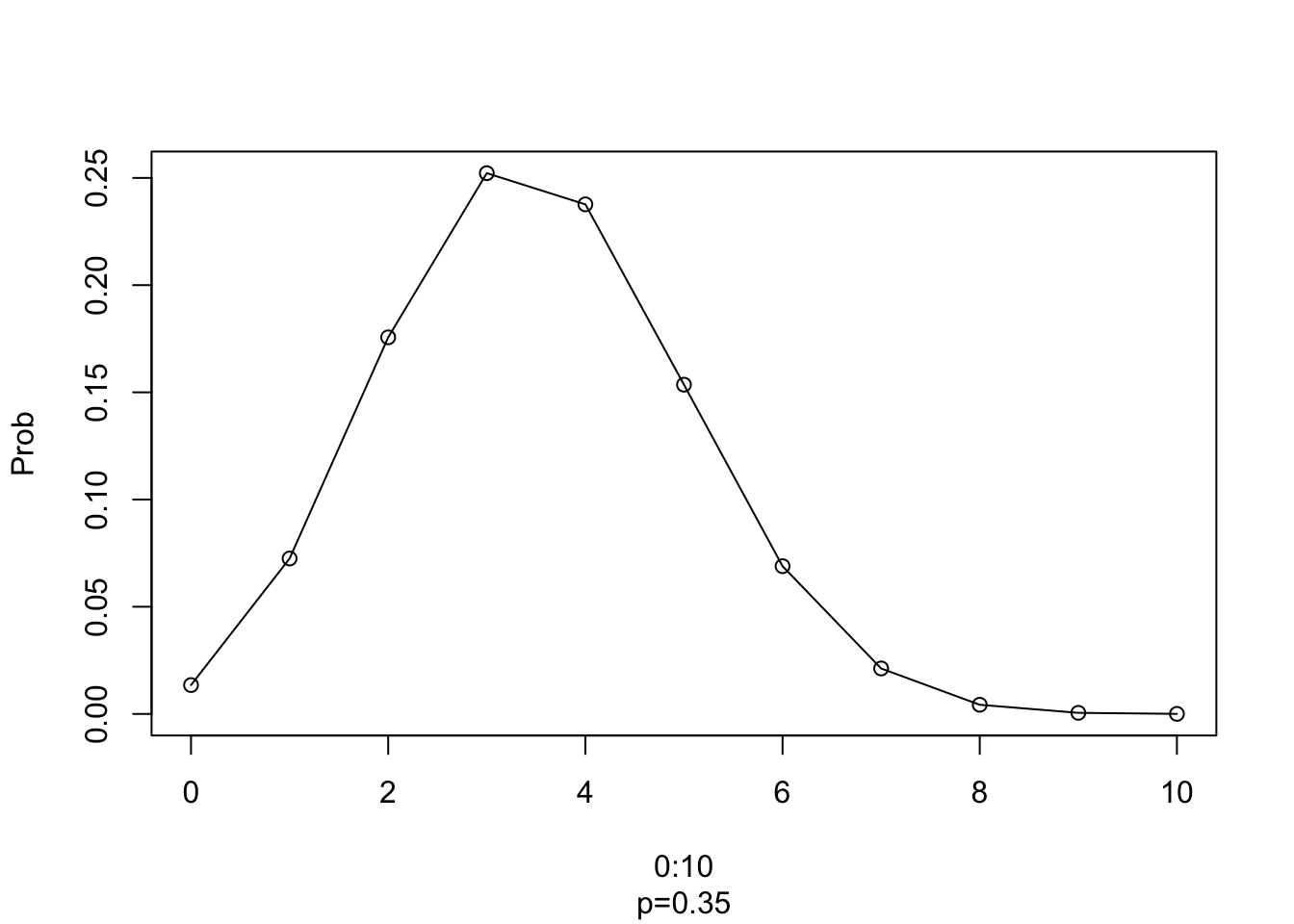
Plot de la distribucion binomial, para n = 0:10; x = 10, p = 0.35.

Figura 6.5: Plot de la distribucion binomial, para n = 0:10; x = 10, p = 0.35.

6.5.9 Obtenga un cuadro resumen utilizando la funcion cbind(., ) de sus resultados.**

Graficar resultados con funciones que involucren la función acumulada

6.5.10 Se realizan de 0:10 intentos de una variable “x” que sigue una distribucion binomial, y se tiene que la probabilidad de que ocurra el evento es 0.65. Cual seria la probabilidad de que menos de 7 eventos ocurran en los 10 ensayos tratados.**

Solución.

n = 0:10; x = 10 ensayos; p = 0.65; q = 0.35.

plot(0:10, pbinom(0:10,10,0.65),type="s" ,xlab="0:10",ylab= "Prob", sub="p=0.65")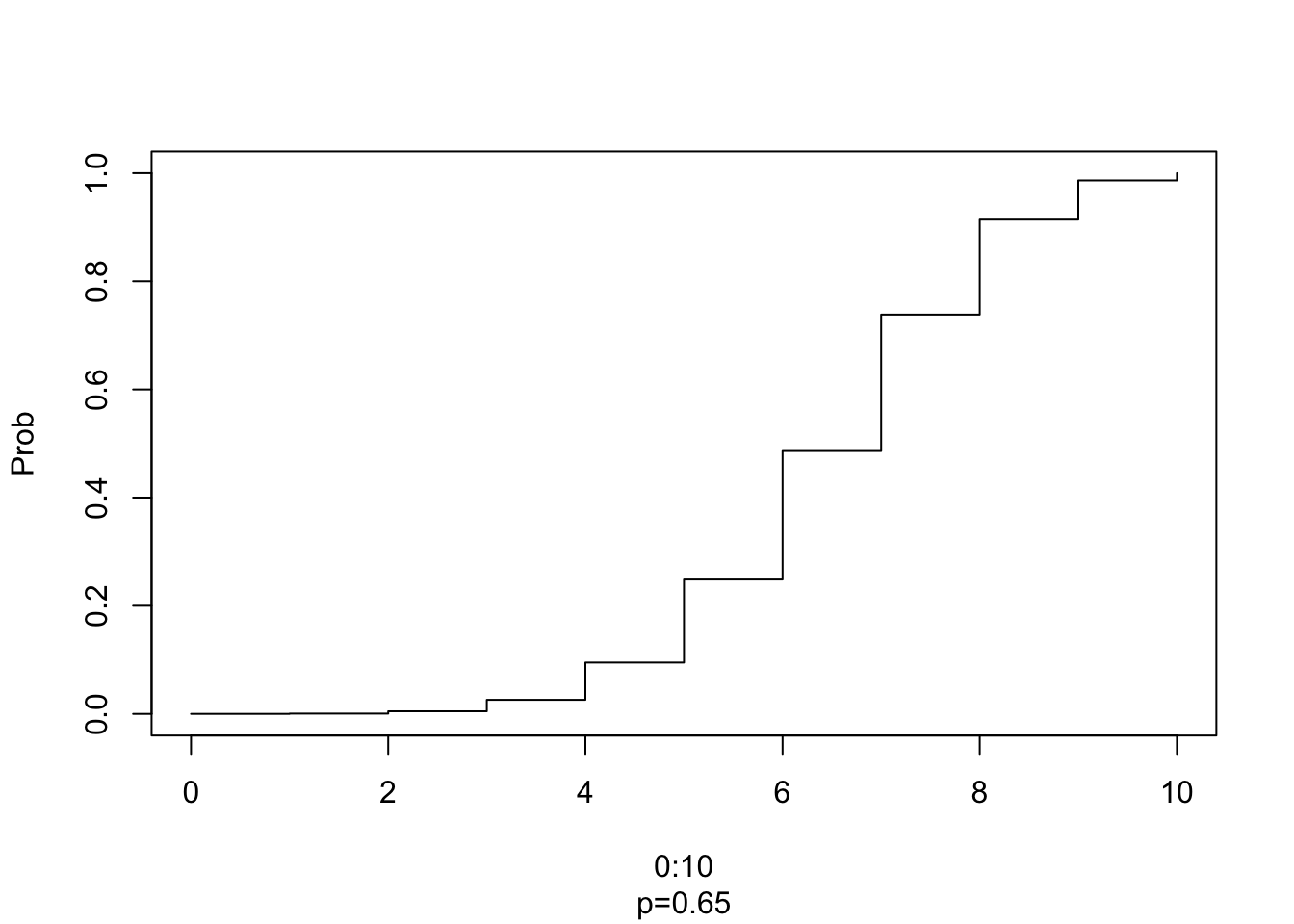
Plot de la distribucion binomial, para n = 0:10; x = 6, p = 0.65.

Figura 6.6: Plot de la distribucion binomial, para n = 0:10; x = 6, p = 0.65.

6.5.11 Se realizan de 0:10 intentos de una variable “x” que sigue una distribucion binomial, y se tiene que la probabilidad de que ocurra el evento es 0.65. Cual seria la probabilidad de que Por lo menos de 7 eventos ocurran en los 10 ensayos tratados.**

Solución. n = 0:10; x = 10 ensayos; p = 0.65; q = 0.35.

plot(0:10, 1-pbinom(0:10,10,0.65),type="s" ,xlab="0:10",ylab= "Prob", sub="p=0.65")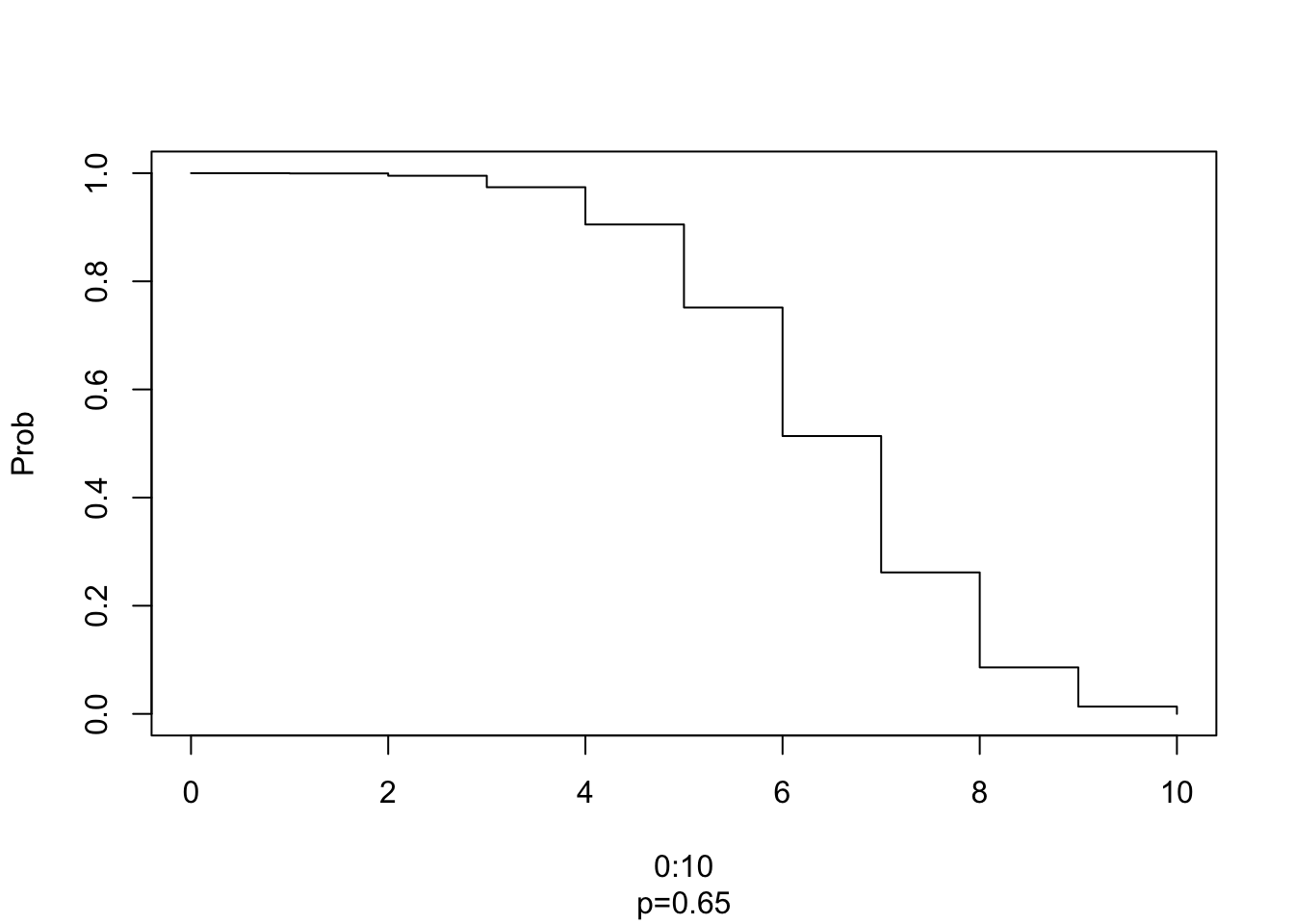
Plot de la distribucion binomial, para n = 0:10; x = 6, p = 0.65.

Figura 6.7: Plot de la distribucion binomial, para n = 0:10; x = 6, p = 0.65.

6.6 Distribución Poisson

La distribución Poisson se presenta en muchos contextos biológicos. Algunos ejemplos de variables aleatorias que presenta distribución poisson son:

. Numero de crías que tiene un individuo de una especie x

. Numero de arboles producidos en una superficie de tierra

. Accidentes en carreteras en un lugar especifico.

. Aparición de una especie rara en un sitio dado.

. Número de colonias de bacterias en una placa de Petri.

. el numero de sustituciones de bases de nucleotidos de un gen en un periodo de tiempo.

. Numero de temblores en un sector y tiempo dado.

Como nota, se trata de eventos raros o poco casuales, que resultan difíciles que se vuelvan a repetir en un tiempo x.

Es una distribución discreta al igual que la distribución binomial, y solo tiene un solo parámetro de la media que se le denomina Lambda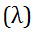

6.6.1 Supongamos que deseamos describir la probabilidad resultante de 0 a 10 intentos, cuando se conoce que la media es de 0.2***

Solución.

x<-0:10  #numero de eventos
x
##  [1]  0  1  2  3  4  5  6  7  8  9 10
y<-dpois(0:10,lambda=0.2)    #funcion en masa
data.frame("Prob"=y,row.names=x)
##        Prob
## 0  8.19e-01
## 1  1.64e-01
## 2  1.64e-02
## 3  1.09e-03
## 4  5.46e-05
## 5  2.18e-06
## 6  7.28e-08
## 7  2.08e-09
## 8  5.20e-11
## 9  1.16e-12
## 10 2.31e-14
plot(0:10, dpois(0:10,0.2), type='h', xlab="intentos",ylab="Probabilidad" )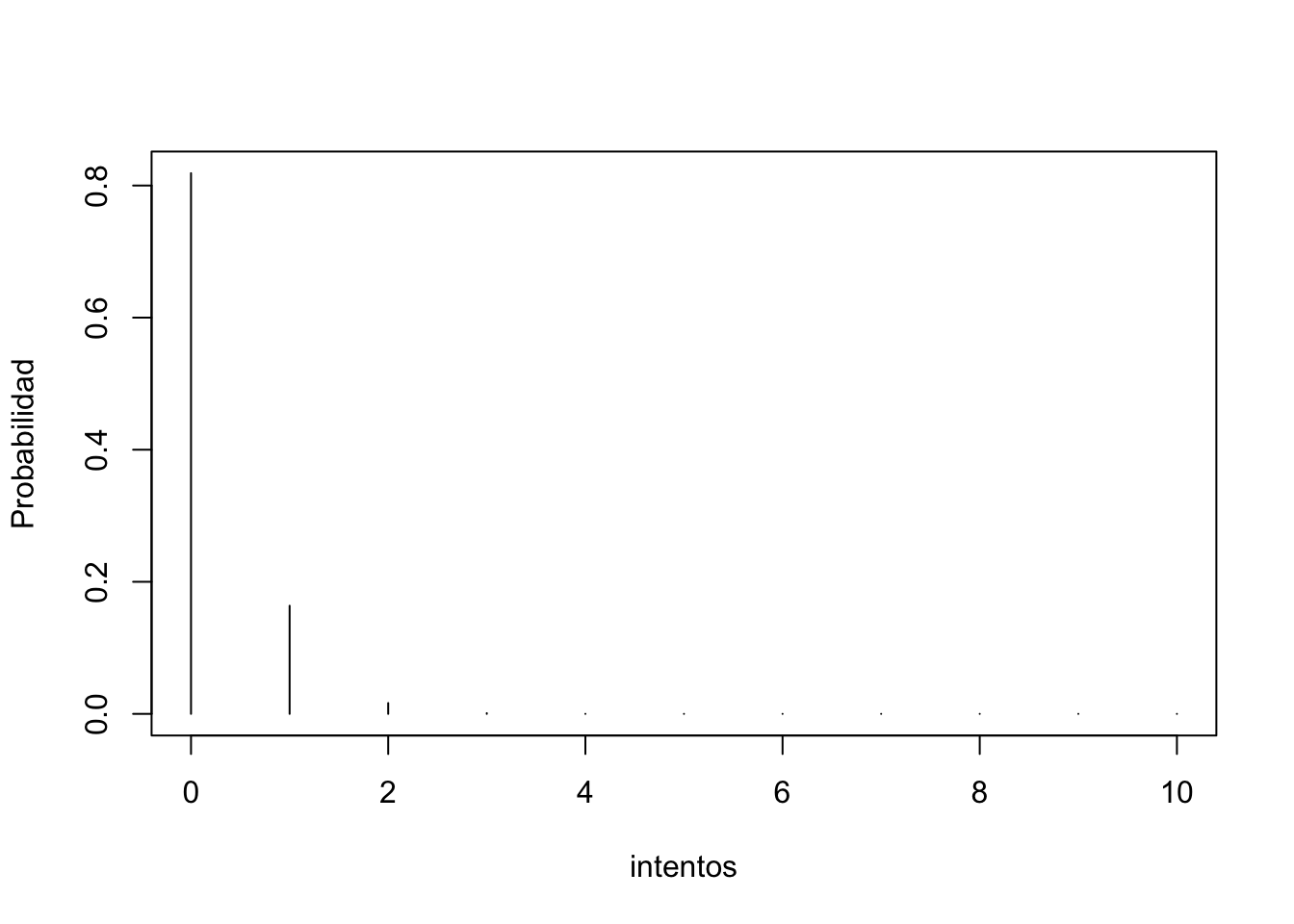
Plot de la Distribucion Poisson

Figura 6.8: Plot de la Distribucion Poisson

6.6.2 En una intersección de carreteras ocurren en promedio 3 accidentes de transito por mes. Calcule las probabilidades de que en un mes cualquiera ocurra:***

6.6.3 exactamente 6 accidentes.**

Solución.

dpois(6,3)
## [1] 0.0504

6.6.4 entre 5 y 15 accidentes.** Solución.

ppois(15,3)- ppois(4,3)
## [1] 0.185

6.6.5 Supongamos que el numero de plantas individuales de una especie dada que esperamos en cien metros cuadrados sigue la distribución de Poisson con una media = 10.***

6.6.6 Determine cual es la probabilidad de encontrar esa misma planta 12 individuos, en otra parcela del mismo tamaño.

Solución.

dpois(12, 10)
## [1] 0.0948

6.6.7 Cual es la probabilidad de encontrar al menos 15 individuos?**

Solución.

1-ppois(14, 10)
## [1] 0.0835

6.6.8 Cual es la probabilidad de encontrar 3 o mas individuos?**

Solución.

1-ppois(2, 10)
## [1] 0.997

Para los ejercicios anteriores, elabore los plot correspondientes a cada ejercicio.